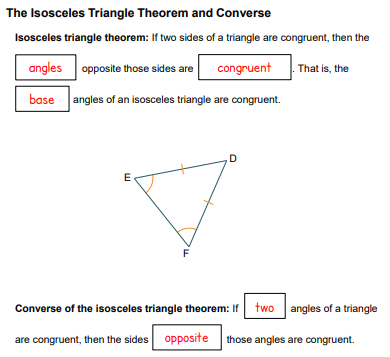
UNIT 4 LESSON 2: ISOSCELES TRIANGLE THEOREM AND ITS CONVERSE
ISOSCELES TRIANGLE THEOREM
DIRECTIONS:
1) Use the CIRCLE WITH CENTER THROUGH POINT 
tool to construct a circle with center A that
passes through B.
2) Select the POINT ON OBJECT 
tool. With this tool selected, touch the circle in 2 different spots
to plot two different points, C and D, on the circle itself.
3) Use the POLYGON 
tool to construct the triangle ACD.
How would you classify this triangle by its sides? Why is this?
4) Select the MOVE 
tool. Now touch one blue segment that serves as a side of this triangle.
In the style bar that appears, select the "Aa" icon. Check "Value" to show the length of this segment.
Repeat this action for the other 2 sides as well.
5) Use the ANGLE 
tool to find and display the measures of all 3 angles of this triangle.
tool to construct a circle with center A that
passes through B.
2) Select the POINT ON OBJECT tool. With this tool selected, touch the circle in 2 different spots
to plot two different points, C and D, on the circle itself.
3) Use the POLYGON tool to construct the triangle ACD.
How would you classify this triangle by its sides? Why is this?
4) Select the MOVE tool. Now touch one blue segment that serves as a side of this triangle.
In the style bar that appears, select the "Aa" icon. Check "Value" to show the length of this segment.
Repeat this action for the other 2 sides as well.
5) Use the ANGLE tool to find and display the measures of all 3 angles of this triangle. When you're done (or if you're unsure of something), feel free to check by watching the quick silent screencast below the applet.
6)
What do you notice? (Be sure to select the MOVE tool again and move all 4 points around!)
Quick (Silent) Demo
CONVERSE OF THE ISOSCELES TRIANGLE THEOREM
Interact with the applet below for a few minutes.
Then, answer the questions that follow.
Be sure to change the locations of the white points and gray point each time
before you re-slide the slider!
CONVERSE OF THE ISOSCELES TRIANGLE THEOREM QUESTIONS
1) Notice how the the triangle was constructed by constructing the green angles first. What is true about the green angles?
2) What else did you notice about this triangle? Explain. (HINT: Think about the sides)
3) Fill in the blanks in the statement below to construct a true statement: If two __________________ of a triangle are _______________, then the ______________ opposite those __________________ are also _________________.
