Aufgabe 2
VIII. Aufgaben
Aufgabe 2
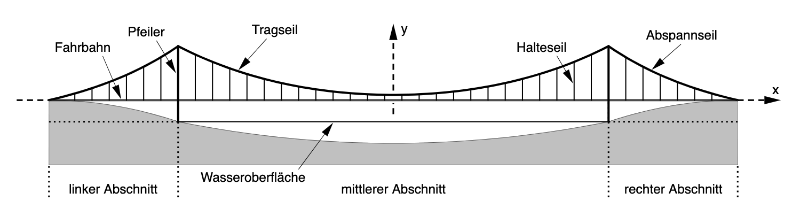
Im schriftlichen Zentralabitur Mathematik 2023 ging es u.a. um den Mittelteil einer Hängebrücke, bei dem für das Tragseil die Funktion
angegeben war.
Eine Längeneinheit entspricht dabei 10m in der Realität. Der Mittelteil ist 400m lang.
a) Berechnen Sie die Höhe des Tragseils über der Fahrbahn an seiner tiefsten Stelle
b) Berechnen Sie die Höhe der Pfeiler über der Fahrbahn.
c) Stellen Sie mit Hilfe der Werte aus a) und b) die Gleichung einer Parabel auf, die durch den tiefsten Punkt und durch die Pfeilerspitzen bzw. verläuft. Bestimmen Sie außerdem die erforderlichen Parameter für eine Kettenlinie, die durch diese drei Punkte verläuft. Zeichnen Sie alle drei Funktionsgraphen mit Hilfe eines GeoGebra-Applets. Welche Funktion dürfte für die reale Konstruktion der Brücke am besten geeignet sein?
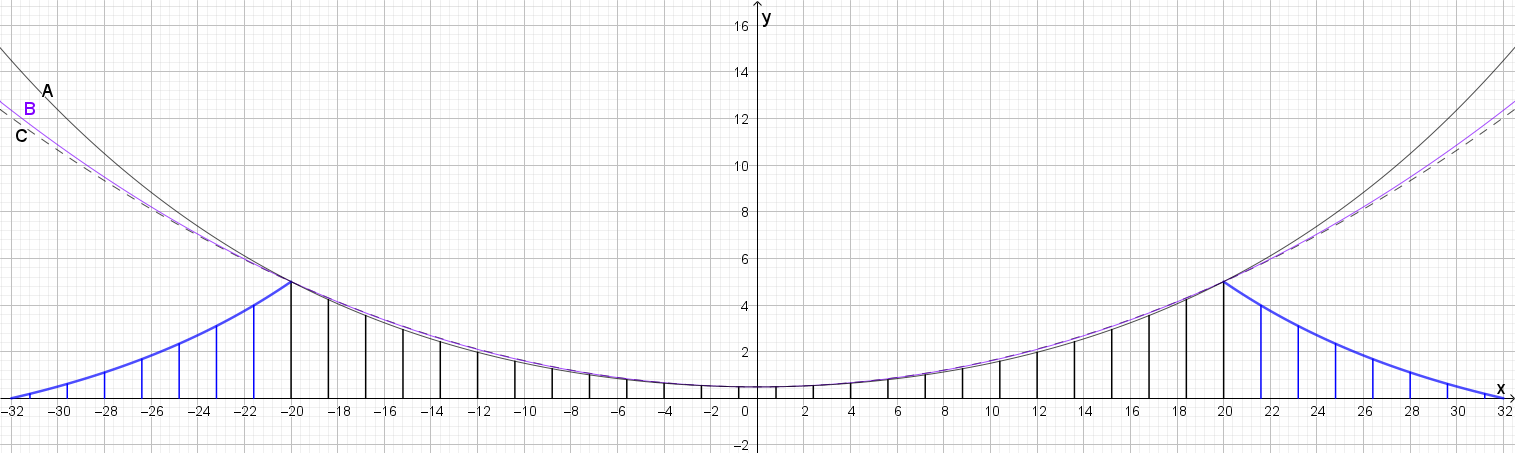
Anmerkung
Während die Parabel (C) und die Kettenlinie (B) außerhalb der Pfeiler nur wenig und zwischen den Pfeilern noch weniger voneinander abweichen, liegt die in der Aufgabenstellung vorgegebene Funktion (A, Polynom 4.Grades) außerhalb der Pfeiler deutlich oberhalb und zwischen Pfeilern und Tiefpunkt noch knapp erkennbar unterhalb von den beiden anderen.
Ein Taylorpolynom 4.Grades für die Kettenlinie würde fast gar nicht von der Kettenlinie abweichen.
So bleibt es das Geheimnis des Autors / der Autorin der Aufgabe, warum gerade diese Funktion s(x) für die Aufgabe gewählt wurde. Zwischen dem Tiefpunkt und den Pfeilern wären einige Halteseile deutlich zu kurz und würden so stärker belastet als andere.