Mathematikwettbewerbe mit GeoGebra angehen
1. Folgen in GeoGebra
In Mathematikwettbewerben werden häufig Aufgaben zu Folgen gestellt. GeoGebra bietet die Möglichkeit, eine endliche Anzahl an Folgegliedern zu berechnen. Der dafür notwendige Befehl lautet
F:=Folge(f,k,a,e),
wobei f die Berechnungsvorschrift der Folge ist, k der Folgeindex, [a,e] das Interval, in dem die Folgeglieder berechnet werden. F enthält dann die Folgeglieder. Beachte den Doppelpunkt vor dem Gleichheitszeichen.
Man kann den Befehl Folge auch verwenden, um ein Array mit den Zahlen von 1 bis 10 zu bekommen.
Darüber hinaus bietet GeoGebra die Möglichkeit, die Elemente eines Arrays A auf eine Bedingung B(k) hin zu prüfen und ein neues Array C zu erzeugen, welches nur die Elemente des Arrays A enthält, die die Bedingung B erfüllen. Die Bedingung muss eine logische Aussage im mathematischen Sinn, also entweder wahr oder falsch sein. Das k ist die Variable in der Bedingung. Für k werden also nach und nach die Werte aus A eingesetzt.
Der zugehörige Befehl lautet
C:=BehalteWenn(B(k),k, A)
2. Beispielaufgabe zum Ausprobieren
Berechnen Sie ein Array mit denjenigen Quadratzahlen, die
1. unter den ersten 10 Quadratzahlen,
2. durch drei teilbar
3. und ungerade sind.
Gehen Sie dabei wie folgt vor:
a. Nutze den Befehl Folge. Die Berechnungsvorschrift der Folge lautet (2*k+1)².
Überlegen dir den Start und den Endwert in Abhängigkeit der Aufgabenstellung.
b. Nutze den Befehl BehalteWenn.
Die Bedingung B für eine durch 3 teilbare Zahl lautet Mod(Divisor,3)≟0. Das Gleichheitszeichen mit dem Fragezeichen ist im Taschenrechner unter #&¬ zu finden. Alternativ kannst du auch zwei Gleichheitszeichen hintereinander setzen.
Fertig?
Bitte klicke das Kästchen an, wenn du mit Aufgabenteil (a) und (b) fertig bist. Du kannst im Anschluss noch Aufgabenteil (c) bearbeiten.
적용되는 모든 것을 선택하세요.
- A
(c) Zusatz: Erstelle einen Schieberegler, mit dem man den Endwert des Folgebefehls einstellen kann. Was fällt dir auf?
3. Wettbewerbsaufgabe
Im Folgenden soll eine von drei Aufgaben bearbeitet werden. Dabei geht es zunächst um das Nachbauen der Applikation. Im Anschluss an das Nachbauen kann, wenn noch Zeit ist, die Bearbeitung der eigentlichen Wettbewerbsaufgabe erfolgen. Dazu wirst du in Zoom in Breakout Rooms eingeteilt.
3.1 Aufgabe zur ebenen Geometrie: Konstruktion eines Dreiecks
Wähle diese Aufgabe, wenn du dich gerne mit ebener Geometrie beschäftigst und/oder in GeoGebra einige Dinge aus den vorherigen Praktika wiederholen möchtest. Die zu erledigenden Schritte sind ausführlich beschrieben.
3.2 Aufgabe zur räumlichen Geomtrie: Teilung eines Würfels in drei Quader
Wähle diese Aufgabe, wenn du gerne in 3D arbeitest und/oder in GeoGebra einige Dinge aus den vorherigen Praktika wiederholen möchtest. Du kannst diese Aufgabe auch wählen, wenn du eine Wettbewerbsaufgabe zum Knobeln bearbeiten möchtest. Die zu erledigenden Schritte der Aufgaben sind hier weniger ausführlich erklärt.
3.3 Aufgabe zu Folgen und Algebra: Zerlegung von 3/n in Stammbrüche
Diese Aufgabe solltest du wählen, wenn du dich schon sehr fit in GeoGebra fühlst und Lust hast, das im ersten Teil des Praktikums erklärte zu vertiefen.
3.1 Aufgabe zur ebenen Geometrie
Es handelt sich um die Aufgabe 3 des diesjährigen Bundeswettbewerb Mathematik.
In einem Dreieck ABC sei ACB = 120°, und die Innenwinkelhalbierenden durch A,B und C schneiden die jeweils gegenüberliegenden Seiten in A' bzw. B' bzw. C'.
Wie groß ist der Winkel A'C'B'?
Anmerkung: Die Richtigkeit des Ergebnisses ist zu beweisen.
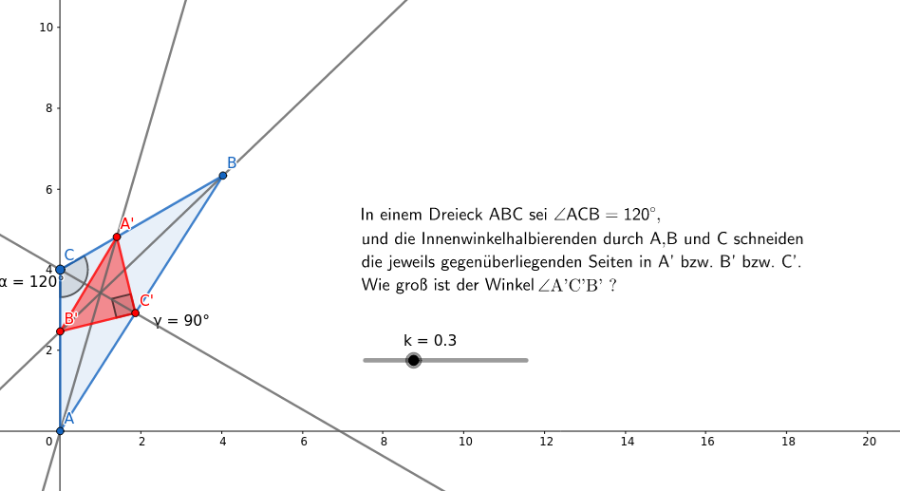
Aufgabe
(a) Baut die Applikation im vorherigen Bild mithilfe der nachfolgenden Anleitung.
Geht folgendermaßen vor:
1. Die Punkte A und C sind bereits vorhanden.
2. Erstelle im Grafikfenster einen Schieberegler k zwischen 0 und 5.
3. Erstelle im Grafikfenster einen Winkel von 120° am Punkt C. Nennen den entstehenden Punkt X.
4. Erzeuge im Algebrafenster einen Punkt B, der mithilfe des Schiebereglers k zwischen C und X verschoben werden kann. Wenn du nicht weiter weißt, findest du zu diesem Aufgabenteil einen Tipp unterhalb der Applikationsumgebung.
5. Erzeuge nun das Viereck ABC und färbe es wie du magst.
6. Konstruiere die Winkelhalbierenden mit dem entsprechenden Werkzeug.
7. Schneide die Winkelhalbierenden mit den gegenüberliegenden Seiten.
8. Benenne die Punkte entsprechend der Aufgabe in A',B' und C'.
9. Verbinde die Punkte A',B' und C' zu einem Vieleck.
10. Zeichne den Winkel A'C'B' ein.
Tipp
zu 4: B = C+k(X-C)
(b) Wie groß ist der Winkel?
(c) Zusatz: Entwickle eine Idee für den Beweis der Wettbewerbsaufgabe.
Bist du mit allen Aufgaben fertig?
적용되는 모든 것을 선택하세요.
- A
3.2 Aufgabe zur räumlichen Geometrie
Es handelt sich um die Aufgabe 1 des diesjährigen Bundeswettbewerb Mathematik.
Ein Würfel mit Kantenlänge 10 wird durch einen ebenen Schnitt in zwei Quader mit ganzzahligen Kantenlängen zerlegt. Anschließend wird einer dieser beiden Quader durch einen zweiten ebenen Schnitt weiter in zwei Quader mit ganzzahligen Kantenlängen zerteilt.
Welches ist das kleinstmögliche Volumen des größten der drei Quader?
Anmerkung: Die Richtigkeit des Ergebnisses ist zu beweisen.
Beispiel
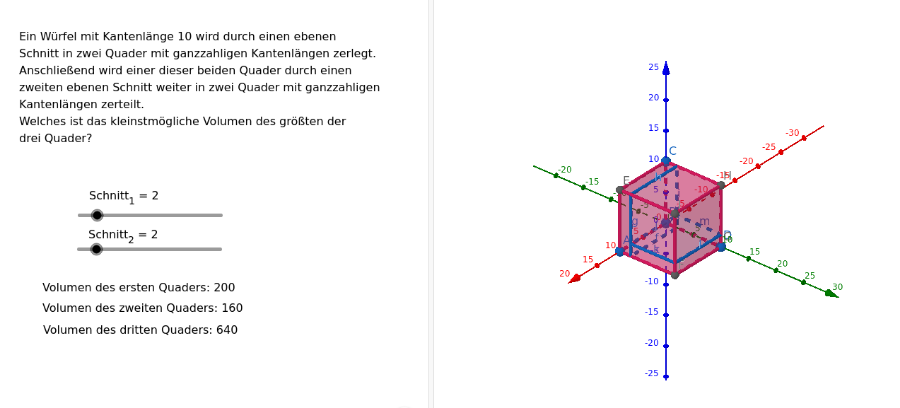
Aufgabe
(a) Baue die Applikation im vorherigen Bild mithilfe der nachfolgenden Anleitung.
Gehe folgendermaßen vor:
1. Ein Würfel mit der Kantenlänge 10 ist bereits erzeugt.
2. Zwei Schieberegler sind ebenfalls erzeugt. Überlege dir mit Bezug auf die Aufgabe, welche (ganzzahligen) Grenzen du den Schiebereglern geben möchtest.
3. Erzeuge im Eingabefenster (ganz unten) eine Ebene F1 (Vieleck) längs oder quer des Würfels, die in dem Würfel liegt und durch einen Schieberegler verschoben werden kann. Dadurch entstehen zwei Quader
4. Erzeuge im Eingabefenster eine zweite Ebene F2 (Vieleck), die in einem der Quader liegt und durch beide Schieberegler beeinflusst werden kann.
5. Erzeuge im Eingabefenster drei Zahlen Q1,Q2,Q3, die die Volumen der drei Quader berechnen.
6. Erzeuge Textfelder, die die berechneten Volumen anzeigen.
Wenn du nicht weiter weißt, gibt es unten Tipps zu einigen Punkten.
(b) Findet die Lösung der Wettbewerbsaufgabe. Erhaltet ihr die gleiche Lösung, wenn ihr die Schnittreihenfolge umkehrt? Warum bzw. warum nicht? Gibt es noch eine weitere Möglichkeit das gleiche Ergebnis zu bekommen?
(c) Zusatz: Wie könnte der formale Beweis aussehen?
Tipps
zu 2:
Die Grenzen sollten 1 und 9 sein, denn ein Schnitt entlang der Kanten des Würfels wäre kein Schnitt.
zu 3:
Das Vieleck kannst du folgendermaßen erzeugen:
F1 = Vieleck((0,S1,0),(10,S1,0),(10,S1,10),(0,S1,10))
zu 4:
Das Vieleck kannst du folgendermaßen erzeugen:
F1 = Vieleck((0,S1,S2),(10,S1,S2),(10,10,S2),(0,10,S2))
zu 5:
Die Berechnungsformeln für die Quader lauten:
Q1 = 10 * 10 * S1
Q2 = 10 * (10 - S1) * S2
Q3 = 10 * (10 - S1) * (10 - S2)
zu 6:
Ein Element aus dem Algebrafenster (z.B. Q1) kannst du über ein Textfeld einbinden, indem du im Texteditor auf Erweitert und dann auf das GeoGebra-Symbol klickst.
Bist du mit allen Aufgaben fertig?
적용되는 모든 것을 선택하세요.
- A
3.3 Aufgabe zu Folgen und Stammbrüchen
Es handelt sich um die Aufgabe 2 b) des diesjährigen Bundeswettbewerb Mathematik.
Der Bruch 3/10 kann auf genau zwei Arten als Summer zweier Stammbrüche dargestellt werden:
b) Gibt es eine nicht durch 3 teilbare positive ganze Zahl n mit der Eigenschaft, dass 3/n auf genau 2021 Arten als Summe zweier Stammbrüche dargestellt werden kann?
Erläuterung: Ein Stammbruch ist ein Bruch der Form 1/z, wobei z eine positive ganze Zahl ist.
Anmerkung: Die Richtigkeit des Ergebnisses ist zu beweisen.

Aufgabe
(a) Baut die Applikation im vorherigen Bild mithilfe der nachfolgenden Anleitung.
Geht folgendermaßen vor:
1. Erzeuge einen Schieberegler für den Exponenten e von N = 2^e.
2. Erzeuge die Folge , mit . Überlege, warum diese obere Schranke sinnvoll ist. Verwende die GeoGebra-Befehle Folge und ceil zum Runde des Endwerts.
3. Untersuche, welche Folgenglieder von F den Zähler 1 haben. Verwende die GeoGebra-Befehle Zähler und BehalteWenn, um die entsprechende Teilfolge zu erzeugen.
4. Bestimmte die möglichen Paarungen als Summe zweier Stammbrüche. Gib Sie und die Anzahl aus. Verwende die GeoGebra-Befehle Länge, Paare und das Werkzeug Text.
Falls du nicht weiter weißt, gibt es unten Tipps zu einigen Punkten.
(b) Wie hängt die Anzahl der Paarungen von der Potenz n ab? Welche Annahme lässt sich damit für die Lösung der Aufgabe ableiten?
(c) Zusatz: Entwickelt eine Idee für den Beweis.
Tipps
zu 2: Der Befehl lautet F := Folge(a-1/k,k,1,ende). Vorher muss a := 3/N und ende := ceil(2*N/3)
zu 3: Der Befehl lautet B := BehalteWenn(Zähler(x)≟1,F)
zu 4: Die Befehl lauten C := a - B, anzahl = Länge(B) und Paare := Folge((B(i),C(i)),i,1,anzahl)
Bist du mit allen Aufgaben fertig?
적용되는 모든 것을 선택하세요.
- A
Puffer: Diskussion
Was hat euch an den Werkzeugen gefallen?
Was hat euch nicht gefallen?
