Problema do tesouro dos Piratas usando Polya
Considere o seguinte problema
Uma história conta que, há muitos anos, o pirata Barba-Ruiva resolveu enterrar seu tesouro. Escolheu uma ilha onde a única praia tinha duas grandes rochas junto à água, e uma enorme palmeira mais distante da praia. Mandou dois dos piratas de seu bando para a palmeira e deu-lhes a seguinte ordem: cada um deveria andar até uma rocha contando os passos. Chegando à rocha, eles deveriam girar 90º, um no sentido horário e outro no sentido anti-horário e andar uma distância igual à que a respectiva rocha estava da palmeira. Nenhum dos piratas se molhou. Os dois piratas ficaram parados e Barba-Ruiva enterrou o tesouro exatamente a meio caminho entre eles. Por acaso, encontramos o documento onde isto estava descrito e resolvemos ir até a ilha à procura do tesouro. Lá encontramos as rochas junto à água, mas, infelizmente, a palmeira havia desaparecido, provavelmente derrubada por um furacão. Como a praia agora é um destino turístico conhecido, não podemos andar e escavar por todo o lado sem levantar suspeitas. A única hipótese é aproveitar uma noite, antes de amanhecer, e fazer apenas um buraco. Onde devemos escavar para descobrir o tesouro?
COMPREENSÃO DO PROBLEMA
- É possível resolver o problema?
- Se for possível, o que é preciso calcular? Ou seja, qual seria a incógnita?
- Quais são os dados? Quais são as condicionantes?
- É possível satisfazer as condicionantes? As condicionantes são suficientes para determinar a incógnita? Ou é insuficiente? Ou redundante? Ou contraditória?
- Separe as diversas partes da condicionante. É possível anotá-las?
- Se não for possível resolver o problema, qual é a justificativa?
- É possível que alguns estudantes achem que não é possível resolver o problema, porque parece que um importante dado (palmeira) não poderá ser usado. Então, peça para que os estudantes provem que o problema não pode ser resolvido.
- Alguns estudantes podem ter dúvidas se o que precisam calcular é uma distância ou coordenadas de um ponto.
- Alguns estudantes podem achar que os dados não são suficientes para resolver o problema. Perguntarão quantos passos há entre as rochas e entre as rochas e a palmeira.
- Alguns estudantes poderão achar irrelevante a informação "Nenhum se molhou".
ESTABELECIMENTO DE UM PLANO
Faça as seguintes questões aos estudantes:
- Você já o viu este problema antes? Ou já viu o mesmo problema apresentado sob uma forma ligeiramente diferente?
- Conhece um problema parecido? Conhece um problema que poderia ser útil?
- É possível representar essa situação num desenho?
- É possível pensar numa adaptação para um problema mais simples?
- É possível modelar a situação no GeoGebra?
- Se os estudantes disserem que já viram um problema parecido, então peça para eles utilizarem a estratégia de resolução neste;
- Se os estudantes não avançarem, peça para fazerem um desenho que possa representar a situação. Disponibilize réguas, compassos, esquadros e transferidores;
- Se não conseguirem avançar após o desenho, peça para considerarem as seguintes distâncias:
- Se não conseguirem avançar peça para modelarem no GeoGebra. Após modelarem, peça para eles arrastarem/mudarem a posição da palmeira e observarem a posição do tesouro. Peça também para mudarem a posição de uma das rochas. Faça-os perceberem que a posição do tesouro não depende da palmeira. Depende de quê então?
- Peça para usarem outras ferramentas do GeoGebra para encontrarem a solução.
- Se não encontrarem a solução, peça para eles construirem no GeoGebra algo parecido com o seguinte:
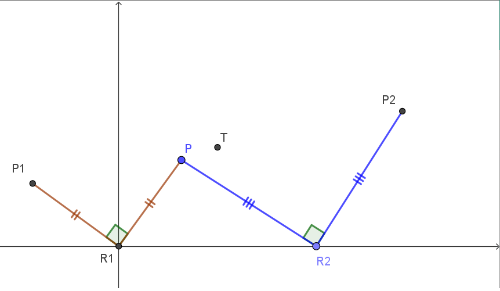 Os eixos são x e y e R1 está na origem.
Os eixos são x e y e R1 está na origem. EXECUÇÃO DO PLANO
Nos comentários anteriores já demos algumas dicas do que pode acontecer na Execução do Plano. Colocaremos mais alguns comentários aqui.
- Se os estudantes não conseguirem avançar muito na resolução você pode auxiliá-los colocando partes da resolução e pedindo para que eles expliquem.
- Pode colocar dicas também. Por exemplo, mostrar a seguinte imagem:
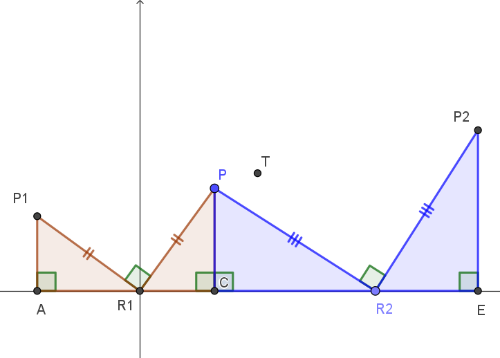
- Se os estudantes não conseguirem fazer, mostre a imagem seguinte:
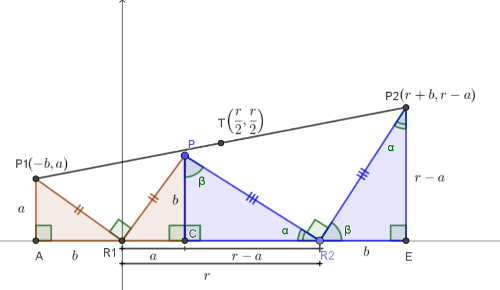
Peça para os estudantes explicarem a resolução apresentada nessa figura.
Peça para os estudantes explicarem a resolução apresentada nessa figura. RETROSPECTO
- Desafie os estudantes a resolverem o problema utilizando outro método. Alguns estudantes de graduação já resolveram utilizando vetores ou coordenadas polares.
- Altere a resolução apresentada anteriormente, colocando R1 na posição (-1, 0). Nesse caso, quais seriam as coordenadas de T?
- Diante do que viram na resolução, peça para os estudantes apresentarem uma orientação de onde devem cavar o buraco para encontrarem o tesouro.
- E se o pirata tivesse falado no final: enterre o tesouro na terça parte entre o pirata 1 e o pirata 2.