Centroids - Composite Area Method
Conceptual Questions - Centroid of a Single Area
How would you expect the location of the x-coordinate, x̄ of the centroid of a rectangle to change if its height is doubled while the width remains the same?
How would you expect the location of the y-coordinate, ȳ of the centroid of a rectangle to change if its height is doubled while the width remains the same?
How would you expect the location of the x-coordinate, x̄ of the centroid of a rectangle to change if its width is doubled while the height remains the same?
How would you expect the location of the y-coordinate, ȳ of the centroid of a rectangle to change if its width is doubled while the height remains the same?
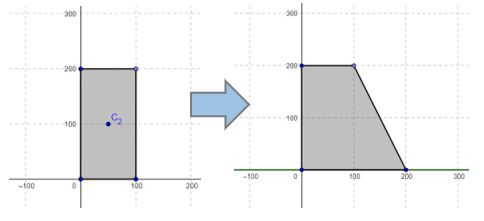
If the rectangle is changed to a trapezoid, how would you expect the location of the centroid to change?
Centroid of a Composite Body
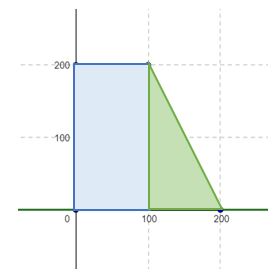
The above trapezoidal composite body can be broken into a rectangle (shape 1) and triangle (shape 2). If the above units are in mm, use the above figure and coordinate system to answer the following questions. What is the x-coordinate of the centroid, x̄1 of the rectangle?
What is the y-coordinate of the centroid, ȳ1 of the rectangle?
The correct expression for the product A1 x̄1 is most nearly...
The correct expression for the product A1 ȳ1 is most nearly...
The x-coordinate of the centroid, x̄2 of the triangle is most nearly...
The y-coordinate of the centroid, ȳ2 of the triangle is most nearly...
The correct expression for the product A2 x̄2 is most nearly...
The correct expression for the product A2 ȳ2 is most nearly...
The location of the centroid of the trapezoid (x̄, ȳ) is most nearly...
If the width of the rectangle were doubled while the triangle remained unchanged, which coordinate of the centroid x̄ or ȳ would you expect to increase by a greater amount?
Use the interactive Figure to Observe Changes in the Centroid of the Composite Body
How would you anticipate the location of the x-coordinate, x̄ of the centroid of the composite shape would change if the area of shape 3 were greatly increased while the others remained the same?
How would you anticipate the location of the y-coordinate, ȳ of the centroid of the composite shape would change if the area of shape 3 were greatly increased while the others remained the same?