Schreibweisen des Differenzen- und Differentialquotienten
Bei der Differentialrechnung handelt es sich um ein Teilgebiet der sogenannten Infinitesimalrechnung. Sie wurde in der zweiten Hälfte des 17. Jahrhunderts unabhängig voneinander durch Gottfried Wilhelm LEIBNIZ (1646-1716) und Isaac NEWTON (1643-1727) entwickelt. (Geschichte der Differentialrechnung)
Durch die zeitgleiche Entstehung auf dem europäischen Festland wie auch den britischen Inseln sind
heute zwei verschiedene Schreibweisen gebräuchlich.
Die uns bereits bekannte Schreibweise sieht folgendermaßen aus:
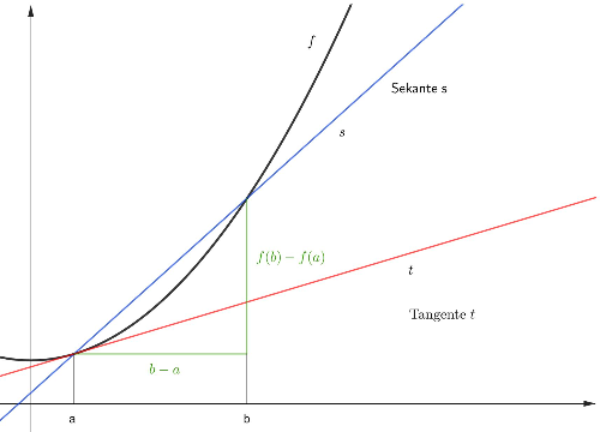
Der sogenannte Differenzenquotient über dem Intervall [a,b] beschreibt die Steigung der Sekante und wird wie folgt gebildet:
Die Steigung der Tangente an der Stelle ist durch den Differentialquotient gegeben:
i) Alternative
Aus dem Physikunterricht ist dir wahrscheinlich die Delta-Schreibweise bereits bekannt.
Man setzt somit wird zu
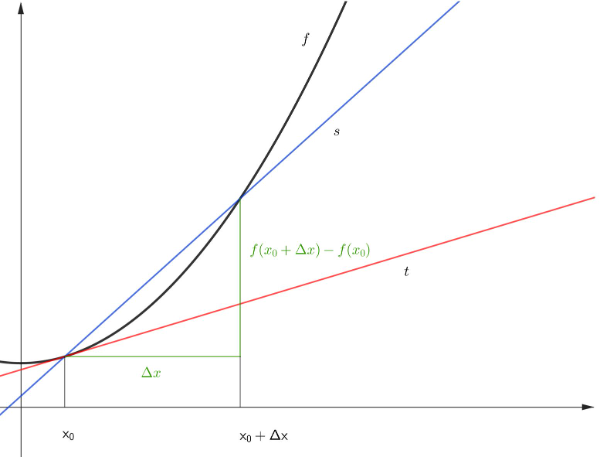
Damit kann der Differentialquotient an der Stelle wie folgt ausgedrückt werden (siehe Abbildung 2):
ii) Leibniz'sche Schreibweise
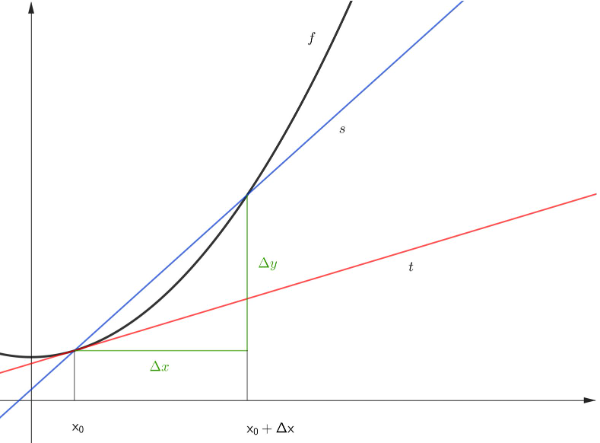
Da der Limes des Differenzenquotienten den Differentialquotienten ergibt lässt sich wie folgt bilden:
Durch diese Grenzwertbildung werden sowohl als auch immer kleiner, man erhält sozusagen "unendlich kleine Größen". Leibniz bezeichnete diese als Differentiale und schrieb sie als dx und dy an.
Der Grenzwert wird dadurch zu
Der Quotient dieser Differentiale ergibt also den sogenannten Differentialquotienten
In der Praxis schreibt man heute oft: [lies: df nach dx]
Diese Schreibweise ist weit verbreitet in Naturwissenschaftlichen Disziplinen wie z.B. der Physik und ist vor allem dann nützlich wenn es auf die genaue Angabe der Stelle nicht ankommt.
________________________________________________________________________________________
Beispiel:
Die Aussage kann also wie folgt angeschrieben werden:
Schreibe die Aussage mit Hilfe der Leibniz-Schreibweise an!
Interpretation
Bei einer Tagesproduktion von x Stück, entstehen einer Firma die Produktionskosten K(x). Interpretiere folgende Aussagen ():