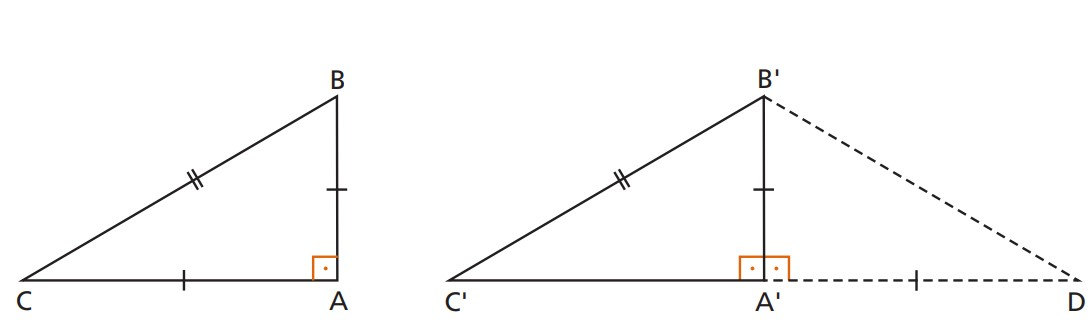
Congruência de triângulos
Dois triângulos são denominados congruentes se for possível estabelecer uma correspondência entre seus vértices de modo que: - seus lados são ordenadamente congruentes aos lados do outro; - seus ângulos são ordenadamente congruentes aos ângulos do outro.
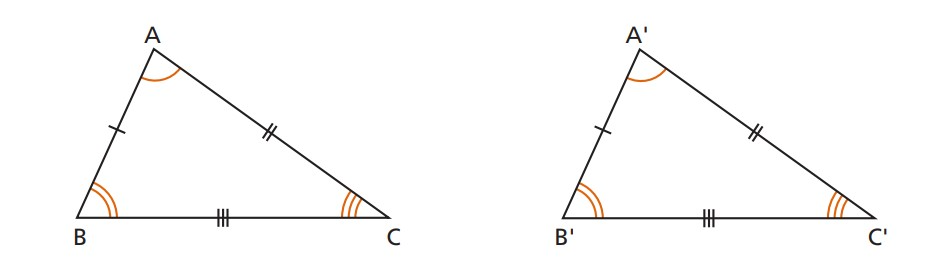
Casos de congruência
Existem condições para que dois triângulos sejam congruentes, estas condições são denominadas casos ou critérios de congruência. 1° - Lado, Lado e Lado (LLL): se dois triângulos têm os três lados respectivamente congruentes, então os triângulos são congruentes.
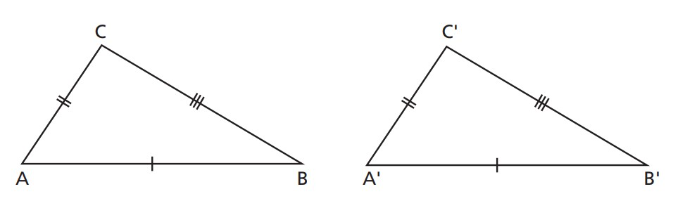
2º - Lado, Ângulo e Lado (LAL): se dois triângulos têm dois lados e o ângulo entre eles respectivamente congruentes, então os triângulos são congruentes.
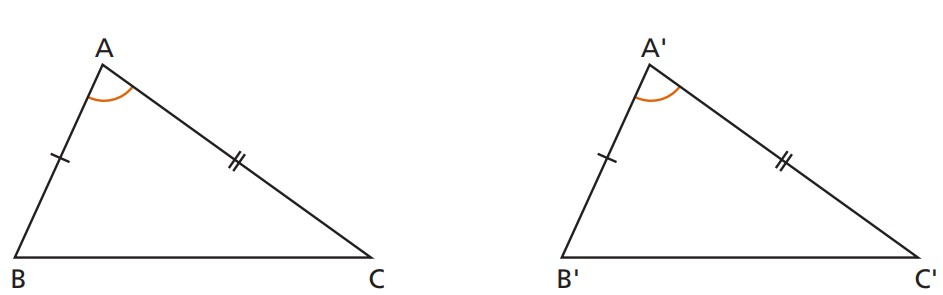
3º - Ângulo, Lado e Ângulo (ALA): caso dois ângulos de dois triângulos sejam congruentes e o lado entre eles também o for, podemos afirmar, que os triângulos são congruentes entre si.
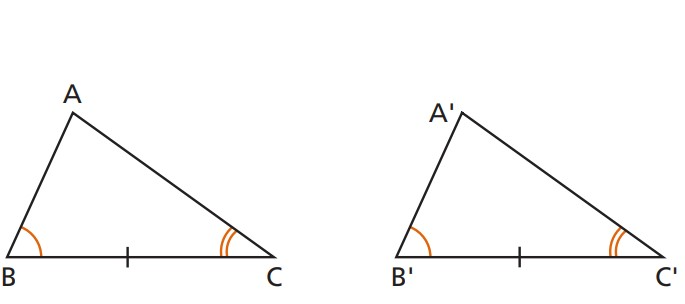
4º - Lado, Ângulo adjacente e Ângulo oposto (LAA): se dois triângulos têm um lado, um ângulo adjacente e o ângulo oposto a esse lado respectivamente congruentes, então os triângulos são congruentes.
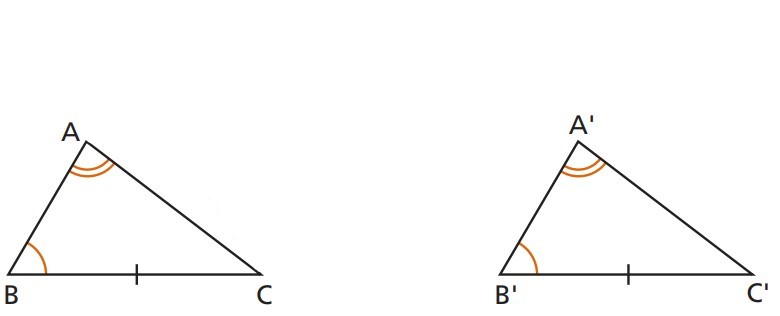
5º - Caso Especial: Se dois triângulos retângulos têm ordenadamente congruentes um cateto e a hipotenusa, então eles são congruentes.