Leckere Verhältnisse und Brüche- Unterrichtsplanung

Kurzinformation
- Thema: Verhältnisse und Brüche
- 5./6. Schulstufe, Mathematik
- Dauer: 3 Unterrichtseinheiten
- SchülerInnenmaterial: Arbeitsaufgabe und Arbeitsblatt für Schüler
- Spezielle Materialien: Kirschsaft, Bananensaft, Schnapsgläser als Messbecher, Lego-Steine, rote und gelbe Tafelkreide, bunte Blätter (grün, gelb, blau)
Vorwissen und Voraussetzungen
Es werden keine speziellen Voraussetzungen benötigt, da es sich um die Einführung in das Thema handelt.
Lediglich der Begriff Bruch sollte aus der Volksschule bekannt sein.
Lernergebnisse und Kompetenzen
Die SchülerInnen können...
- den Zusammenhang von Verhältnissen und Brüchen verstehen.
- ein Verhältnis mit Brüchen beschreiben.
- Brüche addieren und subtrahieren.
- Brüche kürzen und erweitern.
Unterrichtsablauf
Das Thema wird in 3 Unterrichtseinheiten behandelt.
1. Input (durch Lehrer)
2. Mischverhältnisse praktisch erfahren
3. Wiederholung und Zusammenfassung durch Schüler
Der Ablauf der einzelnen Einheiten ist in den einzelnen Unterpunkten beschrieben.
Aktivität 1 (1. Unterrichtseinheit ~50min)
Einführung in das Thema Brüche und Verhältnisse
Es wird mit den SchülerInnen geklärt, was ein Bruch ist und Beispiele genannt. Danach lernen sie, was Kürzen und Erweitern von Brüchen ist und wie es funktioniert. Anschließend kann man mit den SchülerInnen einfache Additionen und Subtraktionen von Brüchen berechnen.
Aktivität 2 (2. Unterrichtseinheit ~50min)
Mischverhältnisse praktisch erfahren.
Schülerarbeit (Dauer ~35min): Die Schüler sollen mit der Hilfe des Arbeitsblattes Mischungen von Kirsch- und Bananensaft erstellen. Dazu werden sie in Gruppen eingeteilt. (Gruppengröße: 3-4 SchülerInnen pro Gruppe). Der genaue Arbeitsauftrag ist dem Aufgabenblatt zu entnehmen. Jede Gruppe erhält ein Aufgabenblatt und eine Tabelle des Arbeitsblattes.
Info für Aufgabenblatt: Pro Gruppe sollen sich die Schüler einigen, welche Mischung sie vermuten. Deshalb genügt eine Tabelle pro Gruppe.
Es ist eventuell notwendig, dass das Kosten der einzelnen KiBa-Mischungen vom Lehrer/von der Lehrerin koordiniert wird.
Auflösung durch Lehrer (~15min): Die Schüler sollen wieder auf ihre Plätze und an der Tafel wird die KiBa-Mischung der einzelnen Gruppen festgehalten, sodass die SchülerInnen dies in ihrer Tabelle eintragen können.
Wichtig: Der Lehrer/die Lehrerin soll dabei zuerst das Verhältnis (z.B. 3 Teile Kirsche, 2 Teile Banane) aufschreiben und dann zur Schreibweise als Buch (3/5 Kirsche 2/5 Banane) wechseln!
Aufgabenblatt - Die Mischung macht's!
Arbeitsblatt für Schüler - Die Mischung macht's!
Aktivität 3 (3. Unterrichtseinheit ~50min)
Wiederholung und Zusammenfassung des Themas Brüche und Verhältnisse.
Ablauf: Man teilt die SchülerInnen in Dreierteams ein. Diese sollen dann auf farbigen Zetteln eine Zusammenfassung zu festgelegten Themen erstellen. Dadurch kann man den Lernerfolg überprüfen.
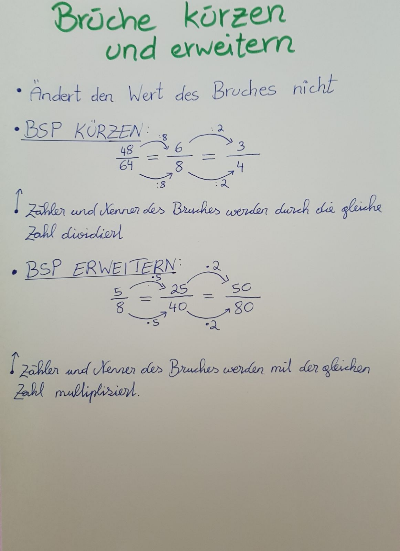
grüner Zettel - Thema 1: Brüche Kürzen und Erweitern
gelber Zettel - Thema 2: Brüche addieren und subtrahieren
blauer Zettel - Thema 3: Brüche und Verhältnisse - Beispiele mit Saft
Jeder Schüler erhält ein Thema, gestaltet sein Blatt und muss es dann seinen Teamkollegen erklären. Das bedeutet: Je ein Schüler/eine Schülerin ist Experte/Expertin für ein Thema in der Gruppe.
Falls die anderen Teammitglieder etwas ergänzen wollen, so dürfen sie das. Nur müssen sie dazu eine andere Farbe zum Schreiben verwenden als der "Experte".
Muster: Grüner Zettel
Muster: Gelber Zettel

Muster: Blauer Zettel

Sicherung / Hausübung
In der dritten Unterrichtseinheit findet die Sicherung der Lernziele statt.
Nachdem man die Zettel der Schüler kontrolliert/verbessert hat, sollen alle Schüler deren Inhalt noch einmal sauber ins HÜ-Heft übertragen.
Überprüfen des Lernerfolges
Man sammelt die farbigen Zettel aus der dritten Einheit ein und sieht sich an, was die Schüler geschrieben haben.
Informationen zum Technologieeinsatz
keine Technologie notwendig
Links zu Materialien und Quellen
Artikel "Die Mischung macht's -KiBa" aus Zeitschrift "Mathematik lehren"
(Ausgabe 179 August 2013 Seite 9)
Methoden vgl. Buch "Mathematik Methodik" von Barzel, Büchter und Leuders.
Link für Aufgabenblatt und Arbeitstabellenblatt

