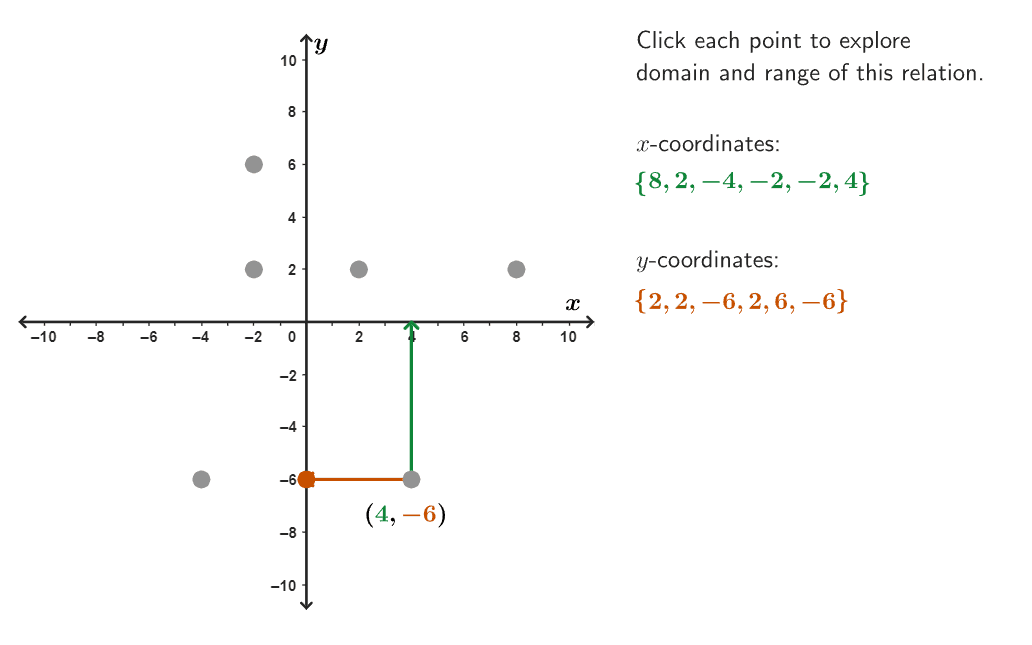Introducing Inverses of Functions
Introducing Inverses of Functions
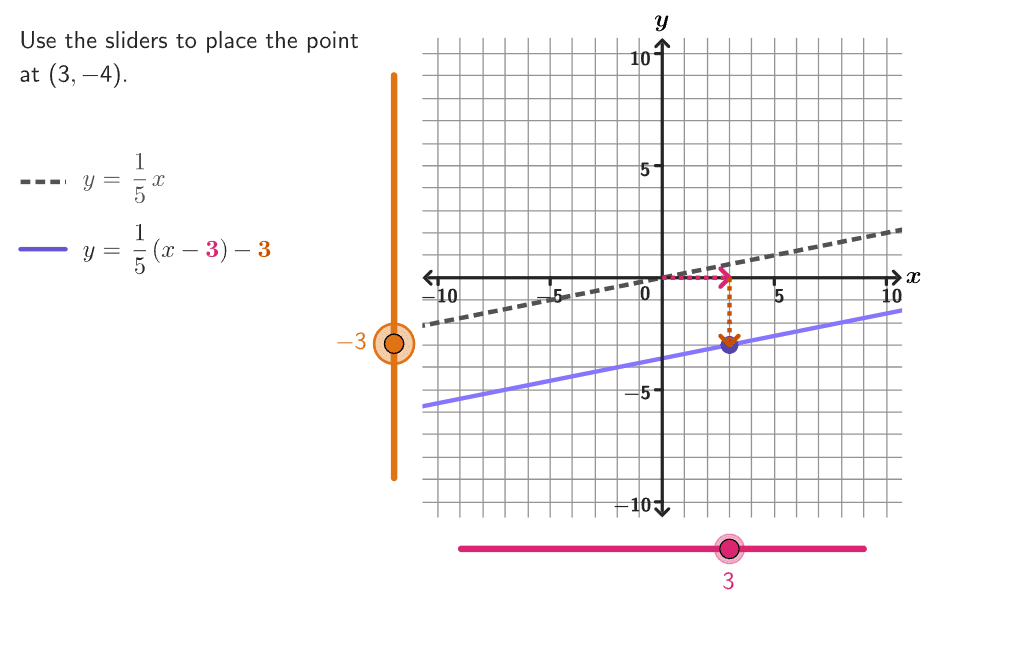
Explore the relationship between a function and its inverse function in this activity.
Author:
Share it with your students:
Exploration
GR. 9-12
Skill:
Find the inverse of a function or relation. Verify that two functions are inverses using their graphs or composition of functions.
Verified resource
Putting It All Together
Answer these open ended questions on your own or with others to form deeper math connections.
Open-ended question 1
What similarities and differences do you notice between the original function and the inverse?
Text and math input
Open-ended question 2
Explain the relationship that the graph of the function and the inverse have with the line .
Text and math input
Open-ended question 3
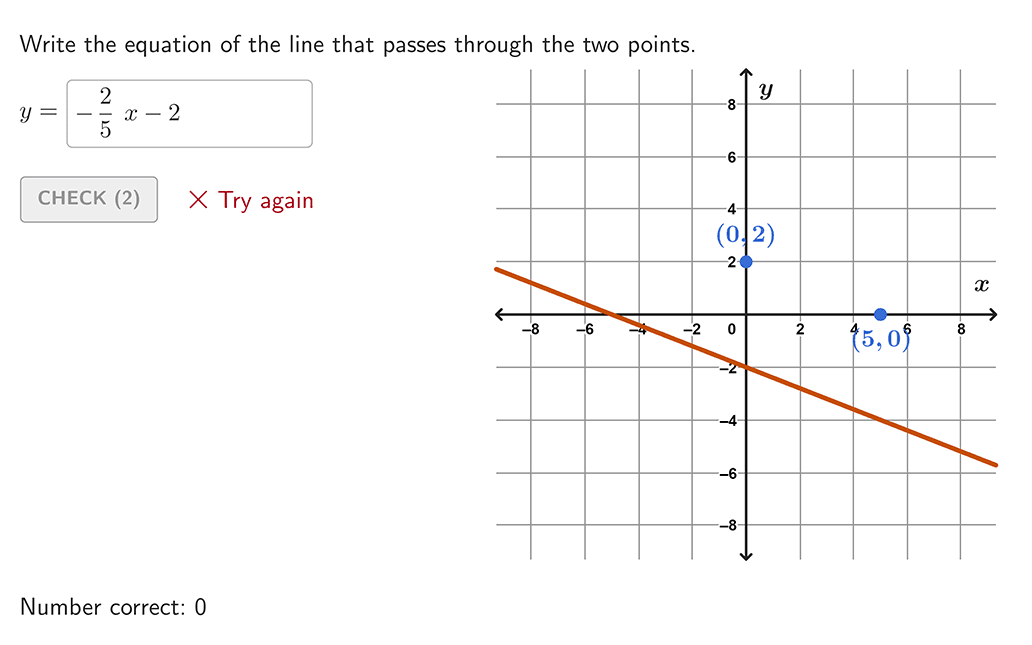
The graph of a linear function passes through and . The graph of another linear function passes through and . Do you have enough information to say that and are inverses of each other?
Text and math input
Open-ended question 4
Could you determine if two functions are inverses if you were given only the first point for each function?
Text and math input
Open-ended question 5
Does have an inverse function? What about if the domain was restricted?
Text and math input
Open-ended question 6
What is an example of a function without an inverse?
Text and math input
Explore more
Prerequisite Resources
