UNIT 4 LESSON 2: ISOSCELES TRIANGLES THEOREMS
THEOREMS AND COROLLARIES OF ISOSCELES TRIANGLES
Fill in the following blanks (based upon your observations). The words to complete these statements can be found in the word bank below. 1) If two sides of a triangle are congruent, then the _____________________ opposite those sides are ____________________. Word Bank: bisector angles congruent perpendicular vertex bisector
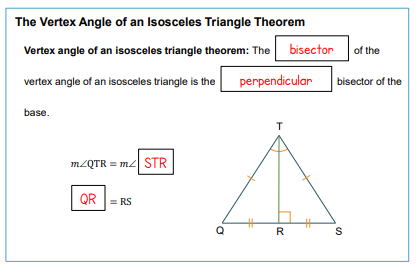
Fill in the following blanks (based upon your observations). The words to complete these statements can be found in the word bank below. 2) The ___________________ of the _________________ angle of an isosceles triangle is the ________________________ ________________ of the base (3rd side). Word Bank: bisector angles congruent perpendicular vertex bisector
I adjusted point D so the measure of angle BAD is equal to the measure of angle CAD.
Which statements are true?
Check all that apply.
-------------------------------------->
THE VERTEX ANGLE OF AN ISOSCELES TRIANGLE THEOREM
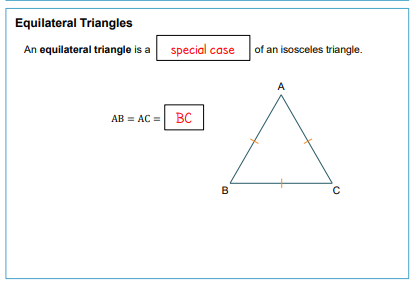
SPECIAL CASE OF ISOSCELES TRIANGLES
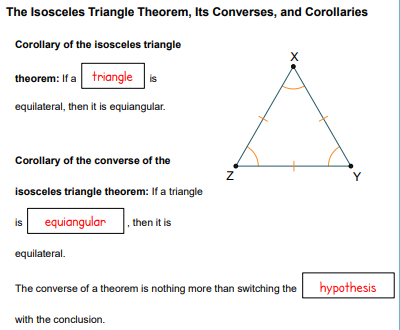
EQUILATERAL AND EQUIANGULAR
 Consider isosceles ΔXYZ. What is the value of n?
Consider isosceles ΔXYZ. What is the value of n?
What is the measure of leg XY? ________ft
What is the measure of leg XZ? ________ ft
 Line segment ZX bisects ∠WZY. If the measure of ∠YXZ is (6m – 12)°, what is the value of m?
Line segment ZX bisects ∠WZY. If the measure of ∠YXZ is (6m – 12)°, what is the value of m?
WHAT YOU SHOULD HAVE LEARNED:
WHAT DID YOU LEARN?