El cristo de la farola (14)
Esta actividad pertenece al libro de GeoGebra G4D en Divulgamat.
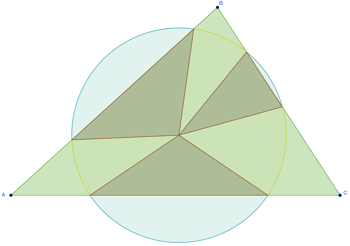
Después de jugar un rato a variar los elementos dinámicos (los vértices, el punto rojo -base de la farola- y el radio de alcance), cayó en la cuenta de que el problema se encontraba también acotado inferiormente.
- Vaya, si el alcance (d) es suficientemente pequeño, no hay dificultad alguna en determinar un punto que no desperdicie luz, pues es fácil situar la farola de forma que el círculo que ilumina caiga completamente dentro del triángulo.
- Justo. Llamando r al radio de la circunferencia inscrita, el problema también está resuelto si d<r.