Teorema de Pitágoras
ROTEIRO DA DEMONSTRAÇÃO
Consideração inicial: este roteiro constitui-se um guia de orientação aos professores.
Hipótese: triângulo retângulo de lados a, b e c, sendo sua hipotenusa de valor a, e seus catetos de valor b e c. α é a medida do ângulo compreendido pelos lados a e b e β é a medida do ângulo compreendido pelos lados a e c.
01- Construir o quadrado de lado b+c a partir de 4 triângulos equivalentes, conforme esboço gráfico.
02- Observar o losango de lado a interno ao quadrado de lado b+c.
03- A soma dos ângulos internos de qualquer triângulo é 180°. Isso implica no argumento de ângulo:α + β = 90°.
04- Marque a opção "Mostrar ângulos". O argumento de ângulo no item anterior implica que, em cada vértice do losango, o ângulo interno é de 90°.
05- Conclusão: o losango de lado a possui os 4 ângulos internos congruentes (de medida 90°), portanto, trata-se de uma quadrado de lado a. Desmarque a opção "Mostrar ângulos".
06- O quadrado de lado a tem área igual a a². Marque a opção "Mostrar texto a²".
07- A região amarelada, interna ao quadrado de lado b+c, tem área igual a a².
08- Argumento de área: realiza-se um movimento rígido em um triângulo retângulo interno de modo que não há sobreposição de regiões e este continua no interior do quadrado de lado b+c; a região amarelada continua tendo área igual a a².
09- Utilizar um dos pontos amarelos para mover apenas um dos triângulos retângulos internos (ao quadrado de lado b+c) . Chame-o de triângulo T1. Observar, segundo o argumento de área, que a região amarelada continua tendo área igual a a².
10- Mova T1 de modo que sua hipotenusa coincida com a hipotenusa do triângulo que lhe é correspondente. Argumento de área: a região amarelada continua tendo área igual a a².
11- Chame o triângulo que não foi movido de T2. Utilize o ponto amarelo correspondente para movê-lo, sem sobreposição de regiões. Argumento de área: a região amarelada continua tendo área igual a a².
12- De forma similar a T1, mova T2 de modo que sua hipotenusa coincida com a hipotenusa do triângulo que lhe é correspondente. Observar que, durante este movimento, há sobreposição de regiões. Portanto, a região amarelada deixar de ter área igual a a². Entretanto, encerrado o movimento, com a hipotenusa de T2 coincidente com a hipotenusa do triângulo que lhe é correspondente, observe que não há sobreposição de
regiões.
13- Argumento de área: a região amarelada continua tendo área igual a a². Desmarque a opção "Mostrar texto a²".
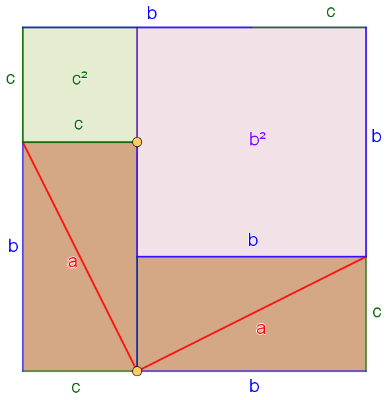
14- Marque a opção "Mostrar quadrados b² e c²". Observe que a região amarelada é perfeitamente preenchida por dois quadrados, um de lado b e outro de lado c, cujas áreas são respectivamente b² e c². Portanto, esta região tem área igual a b² + c².
15- Desmarque a opção "Mostrar quadrados b² e c²". Observe que a região ocupada pelos quadrados de lados b e c é a mesma região amarelada, cuja área é a².
16- Por equivalência de áreas, a² = b² + c². O resultado está demonstrado.
Encerra-se o roteiro de demonstração ao Teorema de Pitágoras.
Figura 1. O losango de lado a é, de fato, um quadrado.
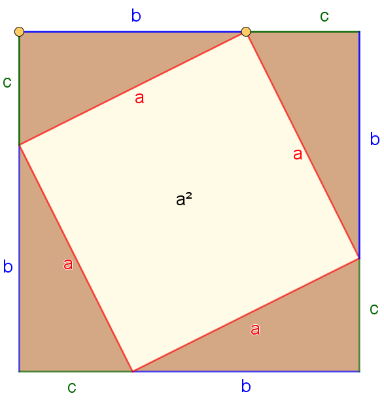
Uma demonstração algébrica
Utilize a Figura 1 para dar uma demonstração algébrica ao Teorema de Pitágoras. Dica: usar produtos notáveis.
Figura 2. Por equivalência de área, a² = b² + c².