Beugung hinter einem Spalt (mit Fresnel-Näherung): Von der Nahfeld zur Fernfeld. Bestimmung der Brennpunkte der Nahfeldbeugung und der Grenzen der Nah-, Übergangs- und Fernbeugungsfelder. (1)
Das Applet untersucht die Beugung hinter einem Spalt für den Fall der Fresnel-Näherung.
Bei der Fresnel-Näherung hängt das Beugungsintegral nur von einem einzigen verallgemeinerten Parameter v ab. Berechnet man die Intensitätsverteilung entlang der Spaltachse als Funktion des Parameters v, so erhält man eine unendlich oszillierende Funktion. Die Abschnitte der Kurve I=I(v) und ihre entsprechenden Extrempunkte werden im Applet in rot/blau dargestellt. Es werden z.B. die ersten 92 Extrempunkte berechnet, die wir als Brennpunkte bezeichnen. v1 - entspricht dem Schirmabstand F1=b2/(2*λ*v12)- dem ersten Brennpunkt. Entsprechend sind v2, v3, ... einige Konstanten in der Fresnel-Näherung, und je nach den Parametern des Problems b, λ, L können die Positionen der Brennpunkte gefunden werden: F1, F2, F3, ... . v1 wird als die Nahfeldbeugungsgrenze betrachtet. Wir nehmen den zuvor gefundenen Parameter ve =0,532126373552312 als Schätzwert für die Grenze der Fernfeldbeugung. Dies ist der Punkt (ve,0) auf der Spaltachse, an dem die Amplitude der Verteilung A=A(v) quer zur Spaltachse in Richtung θ: sin(θ)=b/λ (das erste Seitenminimum der Fraunhofer-Beugung) e-mal kleiner ist als das entsprechende erste Seitenminimum der Verteilung A=A(v) quer zur Spaltachse in Richtung θ für den Punkt (v1,0). Zwischen (v1,0) und (ve,0) nehmen wir an, dass es ein Übergangsfeld gibt .
Es ist zu beachten, dass die Anzahl der Extremwerte der I=I(v)-Verteilung auf der Spaltachse der Fresnel-Näherung unendlich ist. Im Gegensatz zur gleichen Kurve, die auf der Grundlage des Huygens-Fresnel-Prinzips berechnet wurde, ist ihre Anzahl endlich und gleich b/λ. Klicken Sie im Applet auf das Fenster -Zum Vergleich: nach dem Huygens-Fresnel-Prinzip berechnete kritische Punkte v. Die Verteilung I=I(v) quer zur Spaltachse im Nahfeld hat (bei beiden Verfahren) eine endliche Anzahl von Peaks gleich der Ordnungszahl der Brennpunkt (der Schirm wird abwechselnd auf die Brennpunkte aufgesetzt).
Eine erweiterte Version finden Sie im Applet.
1. Tabelle
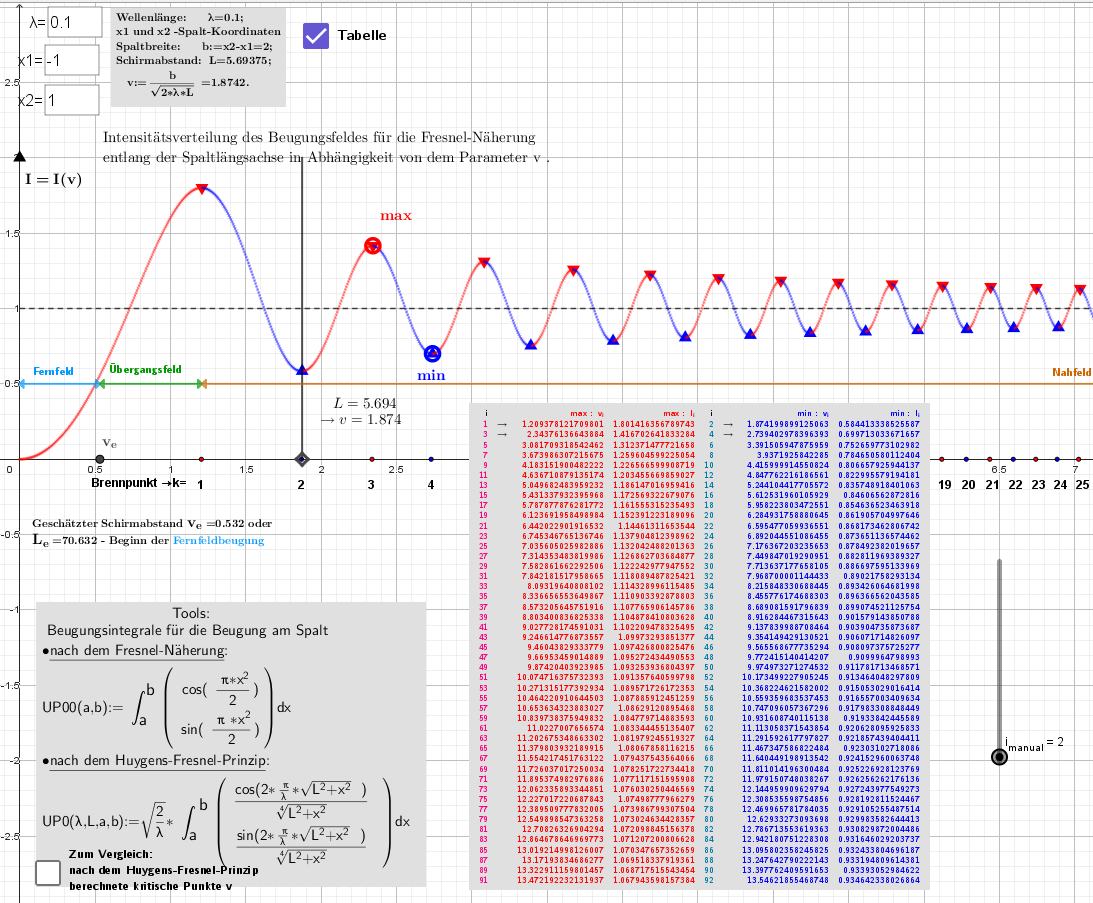
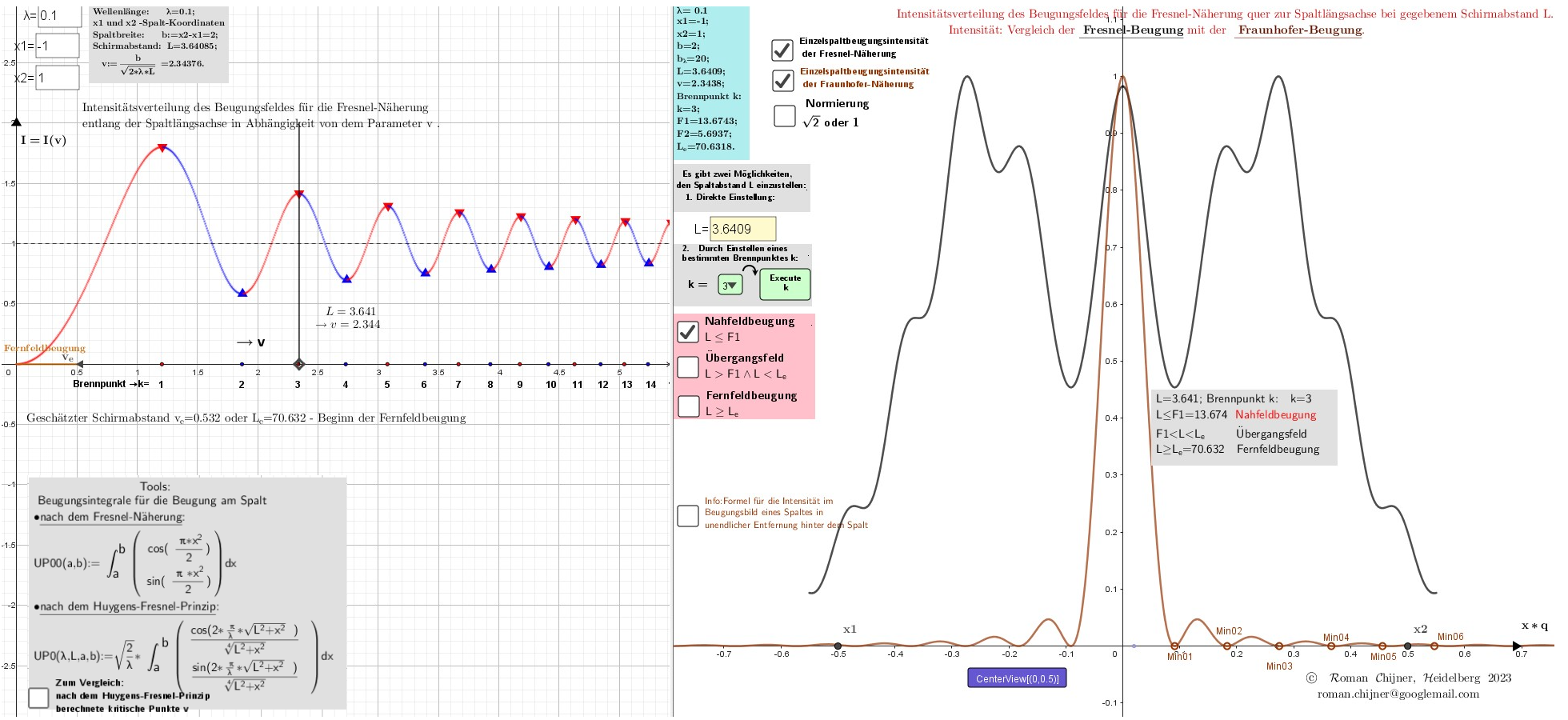
2. Nahfeld: Der Abstand vom Bildschirm zum Spalt L=3.6409, d. h. Der Bildschirm befindet sich im Brennpunkt k=3.
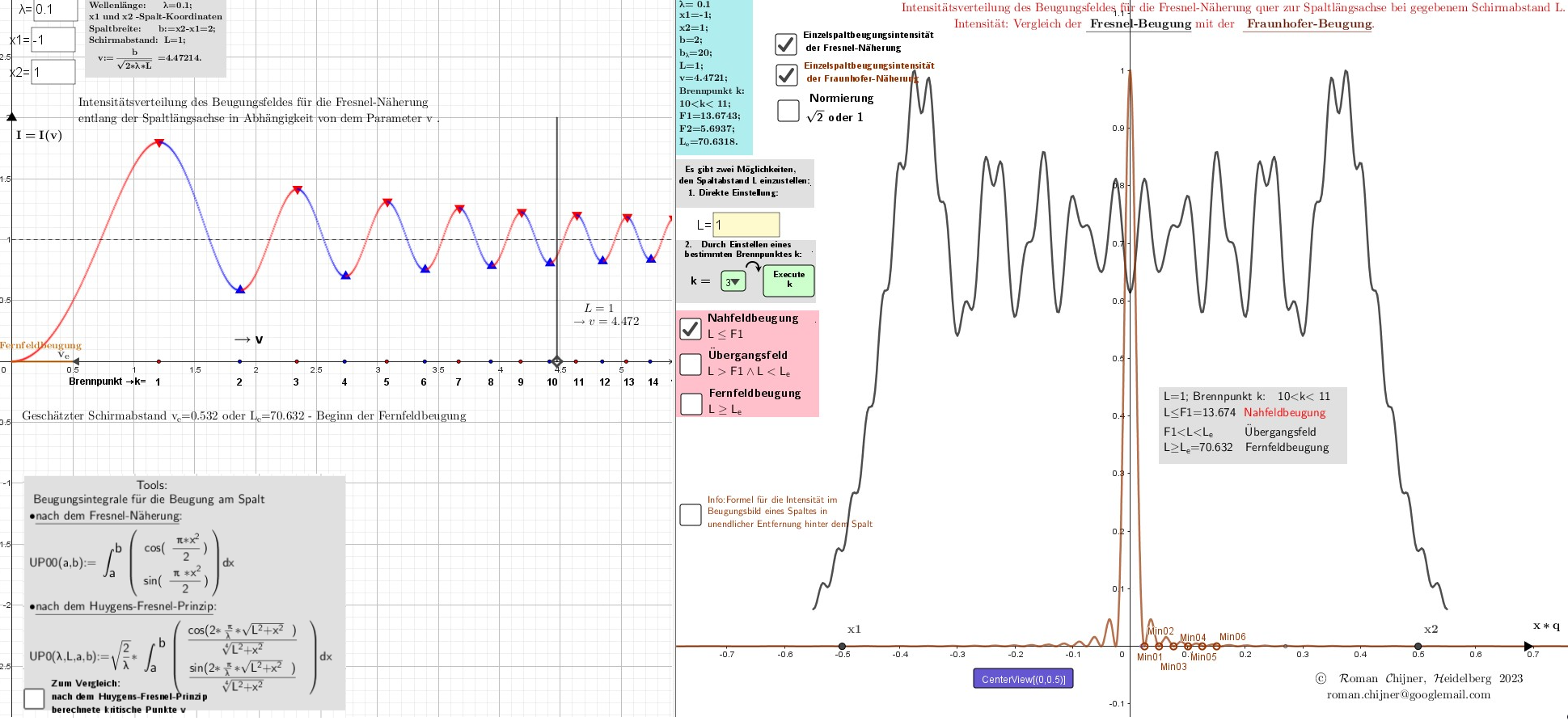
3. Nahfeld: Der Abstand vom Bildschirm zum Spalt L=1, d. h. Der Bildschirm befindet sich zwischen 10 und 11 Brennpunkten.
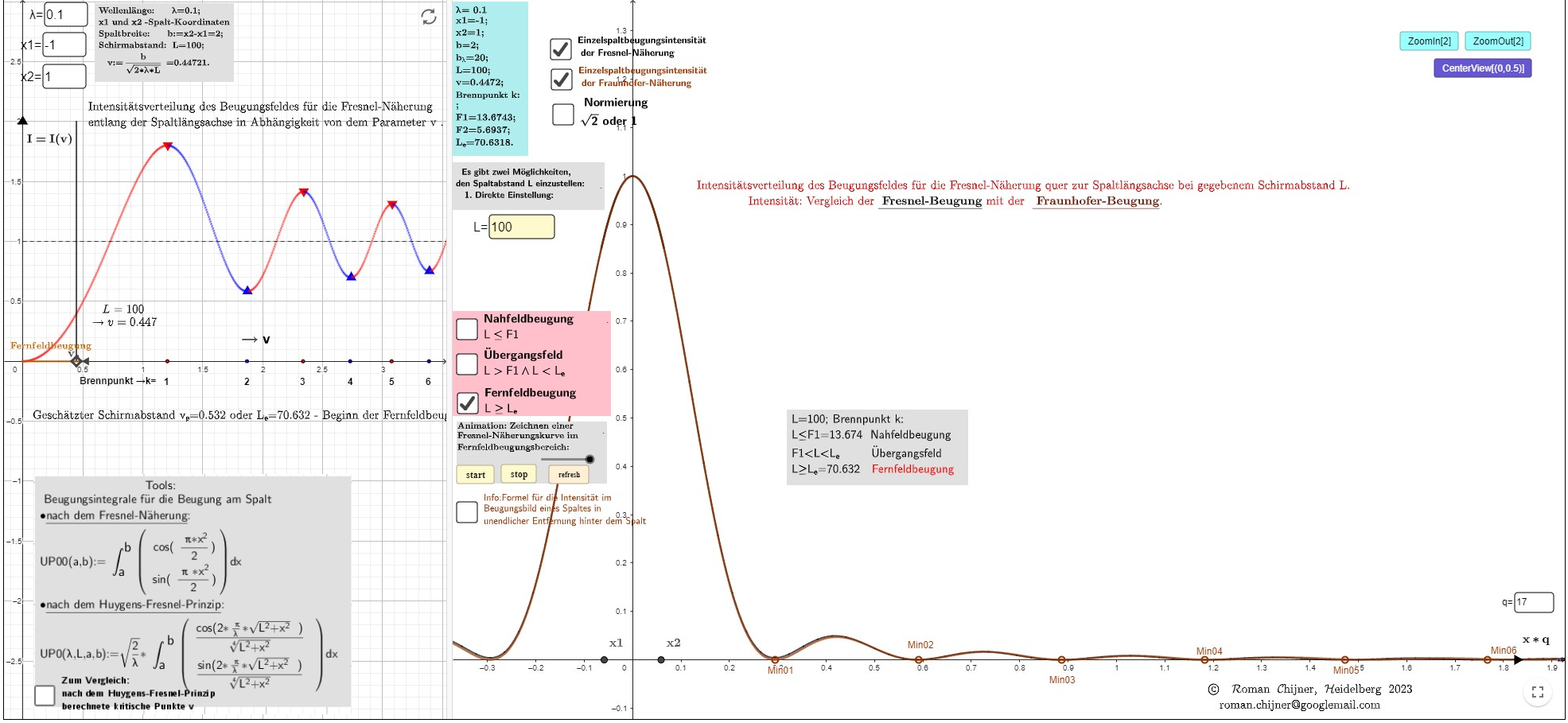
4. Beispiel: Die Übergangsgrenze zwischen Fresnel-Beugung und Fraunhofer-Beugung entspricht einem Wert vₑ=0,5321.
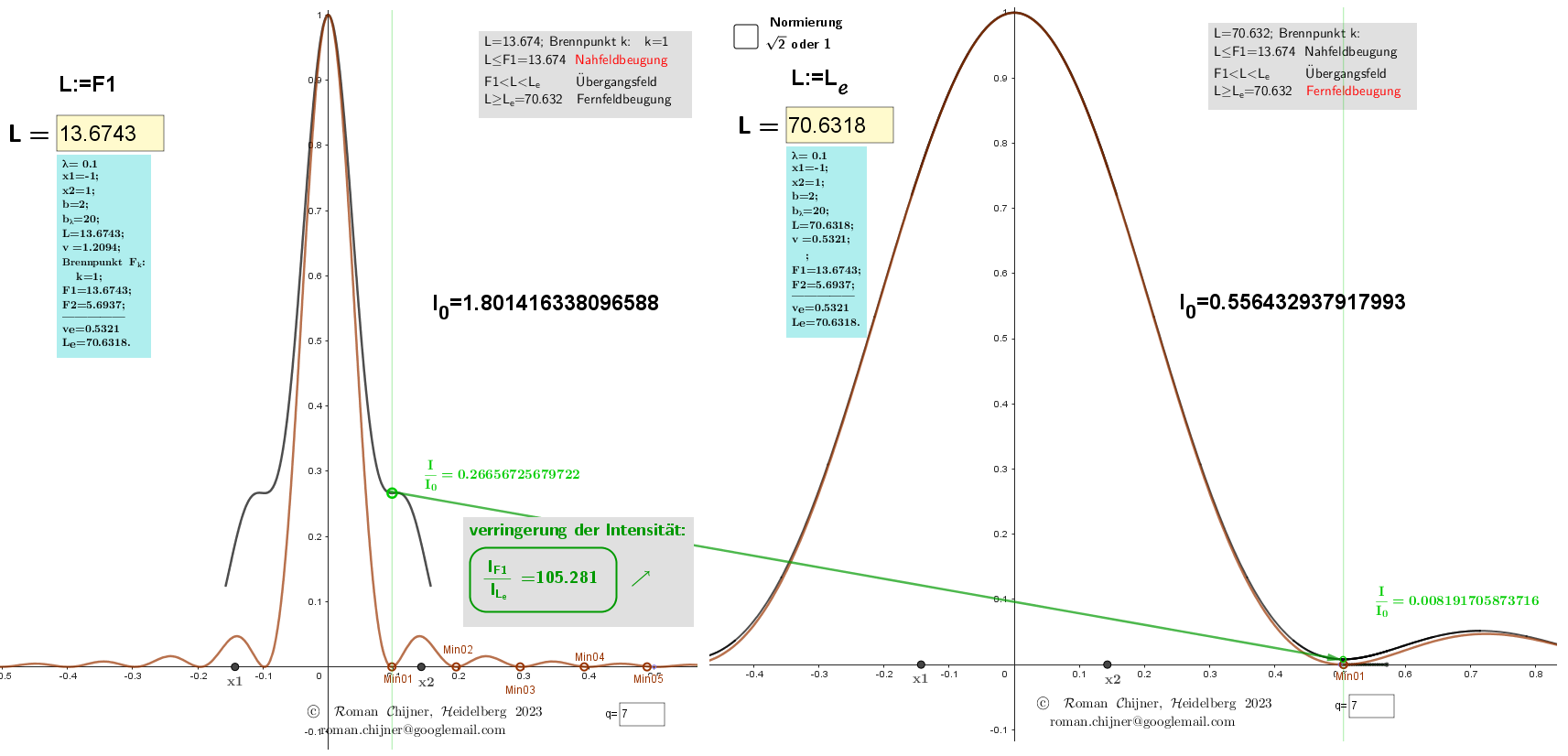
5. Der Fernfeldfall ist die Fraunhofersche Parallelstrahlbeugung. Die Intensitätsverteilungskurve der Fresnel-Approximation und der Fraunhofer-Approximation fallen natürlich zusammen.