Binding Energy
Nuclear Mass
The mass of a nucleus, one might think, is just the sum of the masses of its parts. This seems to stand to reason because if I build a bicycle out of various components, wheels, tires, etc, we always tend to find that the assembled bicycle has a mass equal to the mass of its parts. The same is not true of molecules, atoms or nuclei. The difference is that there is a potential energy of interaction between the parts of the molecular, atomic or nuclear systems. We know from Einstein's work that energy is equivalent to mass, so breaking the whole into it's parts has repercussions on the mass.
The rule in nature is simple: Nature tries to liberate energy by reducing the mass of a system. It is not always able to spontaneously do so, but that's the trend.
A way to quantify the energy that may be liberated by reshuffling the parts is to use the notion of binding energy. Binding energy is just the difference between the mass of the parts and the mass of the whole. For a nucleus, the parts always have higher mass than the whole. Thus
.
It is okay in such calculations to use atomic rather than nuclear masses since the number of electrons wouldn't change, and the associated electron binding energies are around 10 orders of magnitude smaller than the associated nuclear binding energies. The electron rest energies are accounted for if the proton mass is replaced by hydrogen which is made of a proton and a bound electron, and if the element X is an atomic rather than nuclear mass as well. So we could also write.
Binding Energy per Nucleon
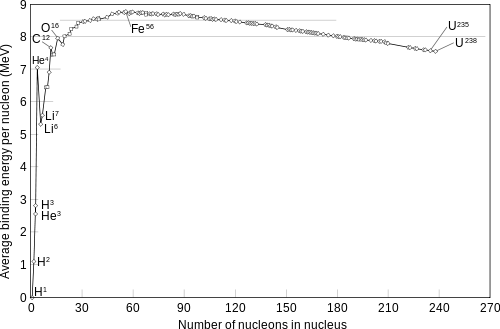
Mass of nuclei are most commonly measured in atomic mass units, denoted 'u'. Since we can equate that mass to units of energy. The common choice of energy unit is the mega-electron volt, or MeV. The conversion is
Some Common Masses
| electron | 5.485 799 090 70(16)×10−4 u |
| proton | 1.007 276 466 879(91) |
| neutron | 1.00866491588(49) |
| H-1 | 1.007825032241(94) |
| Fe-56 | 55.934 937 5 |
| U-238 | 238.050 788 26 |