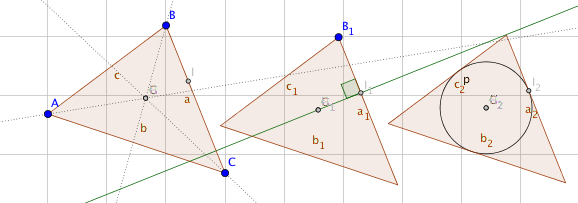
Circuncentro e incentro de un triángulo
Circuncentro
Haced la siguiente construcción en la ventana de abajo:
| Dibuja un triángulo cualquiera. |  |
| Obtén la mediatriz de uno de sus lados haciendo la perpendicular por su punto medio |  |
| Obtén las mediatrices de los otros dos con la herramienta de GeoGebra |  |
| Halla el punto de intersección de las tres rectas mediatrices. Se llama circuncentro. |  |
| Traza la circunferencia de centro el punto anterior y que pasa por los vértices. Se llama circunferencia circunscrita. |  |
| Obtén la distancia a los tres vértices y comprueba que es igual. |  |
| Modifica el triángulo base para comprobar la solidez de la construcción. | |
Incentro
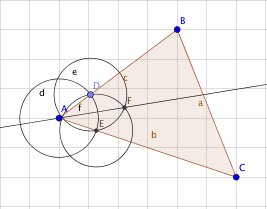
Incentro
Haced la siguiente construcción en la ventana de abajo:
| Dibuja un triángulo cualquiera. |  |
| Obtén la bisectriz de uno de us ángulos usando el procedimiento de las tres circunferencias de arriba. |   |
| Obtén las bisectrices de los otros dos ángulos usando la herramienta de GeoGebra. |  |
| Obtened el punto de intersección. A ese punto se le llama incentro y es el centro de la circunferencia inscrita. |  |
| Halla la distancia de ese punto a los tres lados del triángulo y comprueba que son iguales. |  |
| Dibuja la circunferencia inscrita, para ello traza perpendicular al lado que pase por el incentro y haya la intersección de esa perpendicular con el lado. |    |