4.6.5 Capacidade máxima da calha retângulo-circular

Volume máximo da calha retângulo-circular
Público alvo: Ensino Superior. Objetivo: Abordar um problema de otimização envolvendo a aplicação de uma função quadrática utilizando a metodologia de ensino-aprendizagem-avaliação através da resolução de problemas mediada pelo software GeoGebra. Obs.: O problema da calha é composto por cinco casos.

Situação-problema calha - Caso 5
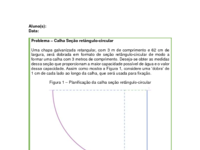
Suponha agora que a mesma chapa galvanizada retangular de 3 metros de comprimento por 62 cm de largura, fosse dobrada em formato de seção retângulo-circular de modo a formar uma calha com 3 metros de comprimento. Quais as medidas dessa seção que proporcionam a maior capacidade possível de água e o valor dessa capacidade? Assim como mostra o aplicativo 'Calha - seção triangular', considere uma ‘dobra’ de 1cm de cada lado ao longo da calha, que será usada para fixação.

Calha - seção retângulo-circular

Você já resolveu os casos anteriores da situação-problema da calha? Caso ainda não tenha resolvido, é interessante que você os resolva para dar continuidade.
Você verificou no aplicativo 'Calha - seção retângulo-circular' que as medidas influenciam na capacidade da calha mesmo o tamanho da chapa sendo fixo?
Que figuras geométricas estão parcialmente representadas no aplicativo? Que função define essa situação? (Use seus conhecimentos sobre área de retângulo e área de círculo).
Utilizando a função definida na questão anterior e as ferramentas do software GeoGebra (janela abaixo), calcule e verifique o valor máximo da capacidade da calha no Caso 5. Qual o valor encontrado?
Considerando a chapa retangular de 3 metros de comprimento por 62 cm de largura, assinale qual das seções abaixo determina sua maior capacidade de água:

Problema Calha - Caso 5 em PDF

Conversando com o professor - Situação-problema da calha