Potencia de un punto respecto una circunferencia

La potencia de un punto respecto una circunferencia recoge tres teoremas de la geometría del círculo, que relacionan los segmentos que se originan al trazar dos rectas cualesquiera desde un punto P, que corten a una circunferencia. Según sea el punto y las rectas, lo denominamos teorema de la(s)

cuerdas, cuando el punto es interior a la circunferencia;
secantes, si es exterior y las dos rectas son secantes;
tangente y secante, cuando una de ellas es tangente. Además, tenemos el teorema de la
altura, que es un caso particular del de las cuerdas, donde una de ellas es un diámetro. En ese cado, sus extremos, junto con un extremo de la otra cuerda forman un triángulo rectángulo. (*) Igualmente, este mismo caso permitiría obtener el "teorema del cateto".

El teorema establece que el producto de las longitudes de los correspondientes segmentos siempre resulta el mismo, independientemente de las rectas elegidas. Tan solo depende del radio de la circunferencia y la distancia del punto al centro. Concretamente, ese producto es la diferencia de sus cuadrados. Ese valor se conoce como "Potencia del punto respecto la circunferencia". Esta sorprendente propiedad resulta muy útil para calcular distancias desconocidas, si podemos relacionar nuestros puntos con una circunferencia. Bastará resolver una pequeña ecuación. Los teoremas se basan en semejanza de triángulos. A veces resulta más cómodo expresar estas relaciones mediante cocientes. En la siguiente actividad podemos visualizar diferentes ejemplos de cada teorema, ver la demostración, y resolver pequeños ejercicios de aplicación directa. Antes de comenzar a resolver los ejercicios, puede resultarte útil echar un vistazo al apartado ¿Cómo averiguar distancias desconocidas?, de más abajo.

Potencia de un punto

Instrucciones

Pulsa el botón "Otro Ejemplo", o bien mueve los puntos de color azul para visualizar diferentes ejemplos.
Marcando la casilla "Valores", podemos ver las longitudes correspondientes.
Además, con la casilla "Cálculos", el valor de los correspondientes productos o fracciones.
La casilla "Usar fracciones" nos permite alternar entre visualizar productos y fracciones.
Con la opción "Las proporciones son redondas", podremos mover los puntos para visualizar situaciones donde no se cumple el teorema.

Ejercicios

Hay dos tipos: calcular el valor de una longitud, o bien colocar un punto para que podamos trazar una circunferencia que pase por todos.
Para todos ellos, habrá que plantear una pequeña ecuación, resultado de la aplicación directa del teorema. Pero ¡cuidado! que en algunos casos habrá que sumar/restar las cantidades obtenidas.
Cada ejercicio correcto vale 1 punto. Las respuestas incorrectas no penalizan.
Podemos hacer tantos ejercicios como queramos. Lo importante es entender bien estos teoremas.

¡Todavía más interesante!

Sabemos que, dado un triángulo, siempre hay una circunferencia (circunscrita) que pasa por sus vértices. Sin embargo, eso ya no es cierto para cuadiláteros, pentágonos, etc... ¿Qué debe cumplir un cuadrilátero para que esto ocurra?, esto es, para que sea "cíclico". Hay diferentes propiedades que lo caracterizan. Por ejemplo, que los ángulos opuestos sean complementarios. También puede verse tomando la intersección de las diagonales o de la prolongación de dos lados opuestos, y comprobando si cumplen el teorema: si los productos de las correspondientes distancias son iguales. Es curioso, porque esto permite relacionar cualquier proporción con una circunferencia:

Si dos razones forman una proporción, entonces al dibujar segmentos de longitud los elementos de esas razones (alineando medios y extremos), tenemos un cuadrilátero por el que pasa una circunferencia, esto es, cíclico.
Si dos razones no forman proporción, entonces ninguna circunferencia contiene pasa por los cuatro puntos.

En la actividad anterior, puedes investigar este curioso hecho marcando la opción Las proporciones son redondas. También lo necesitarás para resolver los ejercicios donde se pide que coloquemos un punto para poder trazar una circunferencia por todos ellos.

¿Cómo averiguar distancias desconocidas?

Ya hemos dicho que estos teoremas nos permiten averiguar distancias desconocidas de una forma sencilla. Pero ¿cómo se hace? Veamos un ejemplo. Supongamos que queremos calcular la distancia entre los puntos A' y B, dada esta situación:

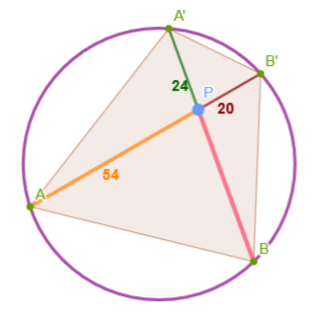
Podemos aplicar el teorema de las cuerdas "potencia de P respecto la circunferencia", denotando x la distancia entre P y B, de manera que

, con lo que .

Con eso ya, la distancia entre A' y B será 45+24=69 (unidades). ¡Sencillo! ¡Anímate y utiliza nuestros teoremas para resolver los ejercicios de propuestos en la actividad interactiva anterior! A veces, los ejercicios son todavía más fáciles y bastará con calcular la distancia de P a B. Resolverlos nos ayudarán a interiorizar el concepto de potencia de un punto respecto una circunferencia.

Un teorema con altura

Por su importancia, es frecuente estudiar el teorema de la altura como un resultado aparte. Podemos enunciar este teorema como:

Dado un triángulo ABC rectángulo en A, sea P el pie de su altura respecto A. Entonces la altura al cuadrado es el producto de los segmentos que origina en la base. Es decir: AP²=BP·PC. La altura es la media proporcional de los segmentos en que divide a la hipotenusa.

Además, si la altura de un triángulo verifica la igualdad anterior, entonces el triángulo es rectángulo en A. Para analizar el teorema desde el punto de vista del teorema de las cuerdas, basta considerar que un triángulo ABC es rectángulo em A cuando el centro de su circunferencia circunscrita yace en la base opuesta BC. (Ver la demostración incluida en el applet)

Por tanto, BC diámetro de la circunferencia.
En particular, el punto simétrico de A respecto BC también está en la circunferencia.
Aplicando el teorema de las cuerdas al pie P de la altura correspondiente a A, tenemos el teorema de la altura.

El teorema del cateto Igualmente, la proporcionalidad entre los segmentos nos permite obtener el teorema del cateto:

La medida del cateto, al cuadrado, es el producto de la hipotenusa por su proyección sobre ella; esto es, Cada cateto de un triángulo rectángulo es media proporcional de la hipotenusa y su proyección sobre ella.

Nuestro turno

A continuación, te proponemos un par de actividades para que puedas poner el práctica lo que acabamos de aprender sobre proporciones y circunferencias (la Potencia de un punto respecto una Circunferencia). Actividad Elige una proporción entre dos razones que quieras (con números sencillos), o bien alguna de las que se obtienen en los ejemplos del applet. 1)

En un folio, utiliza el procedimiento descrito en el apartado ¿Cómo dibujamos una proporción? para representar esta proporción.
Puedes elegir las unidades que te vengan bien, para que el dibujo quepa en tu folio: centímetros, milímetros, o cualquier otra.
Incluye el dibujo de la circunferencia.
- ¿Recuerdas cómo se dibujaba la circunferencia circunscrita para tres puntos?
- Te basta con eso, porque ya sabemos que la circunferencia tiene que pasar obligatoriamente por el cuarto punto.
Puedes probar a dibujar algunas proporciones más.
¿Te ha salido? ¿Tienes dudas? Mira un poco más abajo, por si quieres guiarte en el proceso de creación de una alumna de secundaria.

2) Investiga: Supón ahora que estás diseñando el applet que has visto antes. (*) Este apartado lo realizaremos utilizando un programa de geometría dinámica como GeoGebra.

Sitúa el punto P por ejemplo, en el origen de coordenadas.
¿Cómo podrías hacer para que los segmentos tengan cierta longitud pero "el usuario" pueda modificar la inclinación? (*) Pista, necesitas trazar primero la circunferencia de centro el origen y radio la longitud de ese segmento, y luego situar un punto sobre esa circunferencia.
¿Cómo hacer para que el siguiente punto esté en la misma dirección que el anterior? (*) Pista, necesitas trazar la recta que pasa por el primer punto y el origen.
Dibuja de forma similar los otros dos puntos.
Traza la circunferencia circunscrita utilizando el comando que permite dibujar una circunferencia que pasa por tres puntos. Como teníamos una proporción, ya sabemos que también pasará por el cuarto.

Esta actividad de investigación permite hacer diferentes ampliaciones. Puedes irte fijando en los detalles del applet. Por ejemplo, la circunferencia resultante puede tener un radio "cualquiera" y un centro "cualquiera" ¿Cómo podrías hacer para presentar al final una circunferencia con el centro donde tú elijas, y el radio que tú quieras?

La respuesta está relacionada con hacer traslaciones y homotecias (hay que saber elegir correctamente la razón de semejanza).
Pero, si incorporamos eso, ¿cómo hacemos para permitir que el "usuario" modifique la configuración de los puntos? (*) Pista: una buena idea puede ser utilizar la segunda vista gráfica para hacer todos los cálculos de intersecciones de rectas, distancias, etc., y luego presentar lo que necesites en la vista gráfica 1, utilizando traslaciones y homotecias. Tu profesor puede indicarte la relación que tiene esta forma de trabajar con las funciones: al pasar de una vista gráfica a otra aplicando una homotecia o una traslación, estamos viendo el resultado de aplicar una función, que transforma unos puntos del plano en otros.

Ejemplo

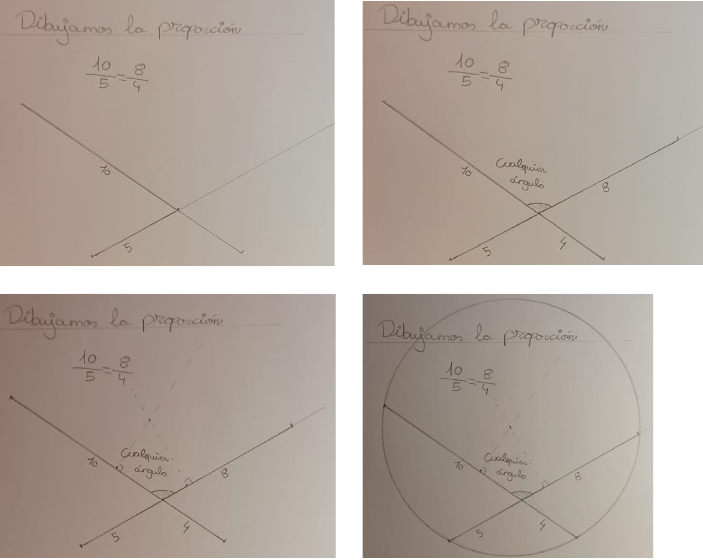
Con las siguientes imágenes, Alicia (IES Albarregas, Mérida), nos muestra el proceso seguido para dibujar la proporción

Imágenes de los personajes del applet, tomadas del proyecto CREA CC BY SA.