Elipsa
Elipsa je skup svih tačaka u ravni takav da je za svaku od njih zbir rastojanja od dveju datih tačaka konstantan.
Te dve tačke se obeležavaju sa i i zovu se žiže ili fokusi elipse. Neka je rastojanje između tačaka i jednako .
Za , tj. ako je dobija se slučaj kružnice.
Neka žiže i pripadaju -osi i neka su simetrične u odnosu na koordinatni početak, tj. neka je i . Označimo sa zbir rastojanja proizvoljne tačke elipse od žiža i , koji je prema definiciji elipse konstantan.
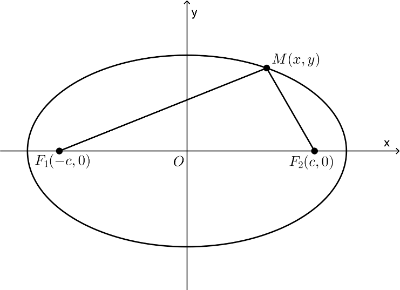
Odnos je numerički ekscentrititet elipse i označava se sa , tj. .
Uz oznaku i osobinu elipse da je zbir rastojanja proizvoljne tačke od žiža elišse i konstantan dobija se jednačina elipse:
.
Ovakav oblik naziva se kanonski oblik jednačine elipse.
Jednačina elipse može biti i u obliku
.
Veličine i nazivamo poluosama elipse. Pri tom, zbog za se kaže da je velika poluosa, a mala poluosa elipse.
Rastojanje žiže od centra elipse naziva se linearni ekscentricitet, i važi .
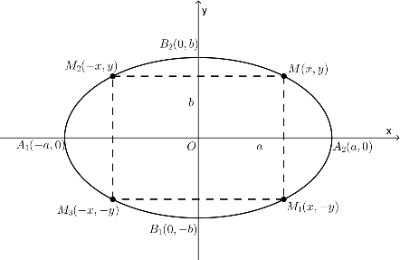
Ako tačka pripada elipsi, tada njoj pripadaju i tačke , i , tj. koordinatne ose su ose simetrije elipse, a koordinatni početak centar simetrije elipse. Tačka je centar elipse.
Tačke takođe pripadaju elipsi i nazivaju se temenima elipse.
Prave čije su jednačine nazivaju se direktrise elipse.
Radijus vektori tačke elipse su dužine
, ,
Parametar elipse je .