Relations in Sets Explained
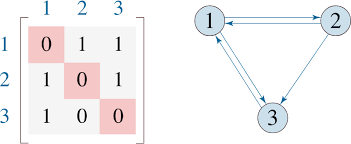
In mathematics, a relation is a set of ordered pairs that establishes a connection or association between elements from two sets. Let's assume we have two sets, A and B. A relation R between A and B is represented as R ⊆ A × B, where A × B is the Cartesian product of A and B, consisting of all possible ordered pairs (a, b) such that a ∈ A and b ∈ B. Relations can be depicted using tables, graphs, or explicit descriptions of the related elements.
Properties of Relations:
There are several properties that relations can possess:
1. Reflexive: A relation R on a set A is reflexive if every element in A is related to itself. In other words, (a, a) ∈ R for all a ∈ A.
2. Symmetric: A relation R on a set A is symmetric if for every (a, b) ∈ R, (b, a) is also in R.
3. Transitive: A relation R on a set A is transitive if, for any elements a, b, and c in A, if (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R.
Relations Set:
The set containing all possible relations between two given sets A and B is denoted as P(A × B), where P denotes the power set (set of all subsets) of A × B. In other words, the relations set is the collection of all subsets of the Cartesian product A × B.
Integer Modulo n:
The integers modulo n, often denoted as Zn, represents a set of integers where each integer is associated with a unique residue class modulo n. Here, n is a positive integer greater than 1, and the set Zn consists of n distinct equivalence classes, each containing integers that have the same remainder when divided by n.
For example, if n = 5, the integers modulo 5 are {0, 1, 2, 3, 4}, where:
- The residue class [0] represents all integers divisible by 5.
- The residue class [1] represents integers that leave a remainder of 1 when divided by 5.
- The residue class [2] represents integers that leave a remainder of 2 when divided by 5.
- The residue class [3] represents integers that leave a remainder of 3 when divided by 5.
- The residue class [4] represents integers that leave a remainder of 4 when divided by 5.
Each residue class in Zn can be represented by a single integer within the range 0 to n-1, and arithmetic operations like addition, subtraction, and multiplication can be performed on these classes in a well-defined manner. The integers modulo n have applications in various fields, including number theory, cryptography, and computer science.