Kopie von Natürliche Logarithmusfunktion: Verhalten an den Rändern des Definitionsbereichs
Auch die natürliche Logarithmusfunktion zeigt eine Besonderheit beim Grenzwertverhalten
Die natürliche Logarithmusfunktion zeigt genau die umgekehrte Besonderheit wie die natürliche Exponentialfunktion:
wächst für "langsamer" als jede Potenzfunktion mit gegen unendlich.
Wir betrachten die Funktion .
Stelle dir wieder die Frage, ob Zähler oder Nenner schneller gegen unendlich wachsen und bestimme anhand dieser Überlegung den Grenzwert
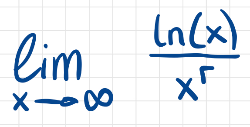
Grenzwertverhalten von h am Graphen von h erkennen
Überzeuge dich davon, dass der oben gesuchte Grenzwert von h tatsächlich 0 ist für alle Potenzen r. Variiere dazu den Wert von r mit dem Schieberegler und beobachte den Graphen von h (blau) im Bereich x gegen unendlich.
Formuliere in eigenen Worten den Zusammenhang zwischen dem Grenzwertverhalten von h für x gegen unendlich und der Besonderheit im Grenzwertverhalten von ln(x).