Psychologische test: modeluitwerking
Een psycholoog beweert een test ontworpen te hebben die de 'aanleg tot statistiek' van individuen kan bepalen. Een leerkracht wiskunde wil nagaan of deze bewering klopt. Hij neemt daarom bij 15 leerlingen, zonder voorkennis statistiek, de psychologische test af (= test 1), laat hen daarna gedurende 5 uur een stukje van de cursus statistiek instuderen, en neemt dan hierover een test af (= test 2). De resultaten van de twee testen vind je in de tabel hieronder.
Goemaere, E., Taecke, D., Wellecomme, S., & Gijbels, G. (2020). Pienter Statistiek Derde graad TSO. Wommelgem: VAN IN.
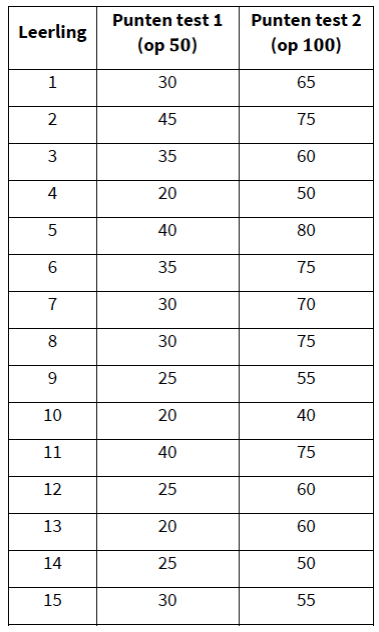
De leerkracht wil nu nagaan in welke mate de punten op de test van de psycholoog (test 1) de punten op zijn eigen test (test 2) kunnen voorspellen. We maken hiervoor een spreidingsdiagram in de grafische rekenmachine van GeoGebra. We plaatsen in de tabel alle waarden van test 1 in de kolom x en alle waarden van test 2 in de kolom . De puntenwolk wordt automatisch getekend in het tekenvenster.
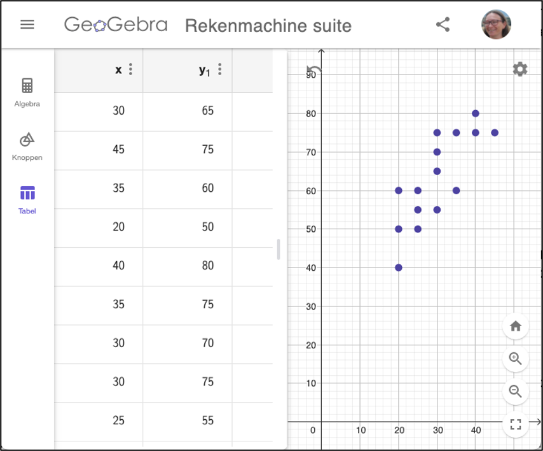
Dit spreidingsdiagram doet vermoeden dat er een redelijk sterke positieve lineaire correlatie is tussen de resultaten van de twee testen. We gaan op zoek naar de correlatiecoëfficiënt door Correlatiecoëfficiënt(x1, y1) in het algebravenster in te tikken.

Ook de correlatiecoëfficiënt geeft dus aan dat er hier sprake is van een redelijk sterke positieve correlatie. Het is dus verantwoord om de regressierechte te zoeken. In het algebravenster tikken we hiervoor het commando Regressielijn((x1, y1)) in. Let op: de dubbele haakjes zijn nodig! De regressierechte wordt automatisch in het tekenvenster getekend.
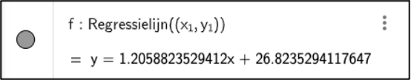
De regressierechte kan je ook vinden vertrekkende vanuit de tabel. Ga naar de drie verticale puntjes bij de kolom y1 en kies voor Regressie. Kies Linear als regressiemodel. Als je daarna op PLOT klikt, dan komt deze functie in het algebravenster en verschijnt de grafiek in het tekenvenster.
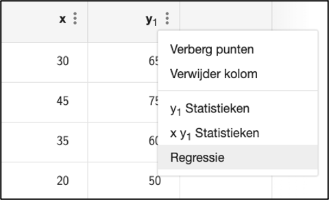
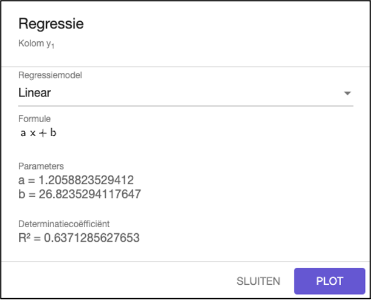
Merk op: in de laatste versie van GeoGebra Suite kan je via de laatste werkwijze ook de correlatiecoëfficiënt krijgen.
De regressierechte kan je uiteraard gebruiken voor inter- en extrapolatie.
- Een resultaat van 32 op de psychologische test (de eerste test) doet vermoeden dat de leerling ongeveer 65,4 zal halen bij de tweede test. Hier is sprake van interpolatie.
- Een leerling die een 10 haalt op de psychologische test zal vermoedelijk ook slecht scoren op de tweede test. We verwachten bij de tweede test en score van ongeveer 38,9. Hier is sprake van extrapolatie.
