Sistemas de ecuaciones lineales y su representación
Ya que sabemos qué es y cómo se grafica una ecuación lineal en GeoGebra. Ahora analizaremos varias ecuaciones lineales a la vez y veremos lo que podremos encontrar.
Cuando analizamos varias ecuaciones de la recta a la vez, estamos hablando de un sistema de ecuaciones lineales, por ejemplo:
2x - 3y = 45 4x - 9y = 2
Ejemplo de sistemas de ecuaciones
Da clic en cada uno de los sistemas sistemas lineales que tienes abajo.
Pregunta
Selecciona la opción correcta, respecto al número de puntos en los que se interseca el: Sistema de ecuación lineal 1: recta1 y recta2
Pregunta
Selecciona la opción correcta, respecto al número de puntos en los que se interseca el: Sistema de ecuación lineal 2: recta3 y recta4
Pregunta
Selecciona la opción correcta, respecto al número de puntos en los que se interseca el: Sistema de ecuación lineal 3: recta5 y recta6
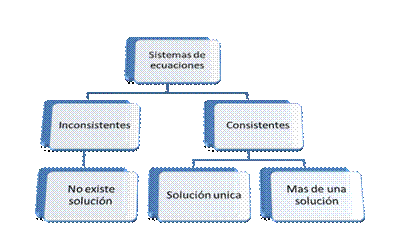
En resumen
Cuando un sistema de ecuaciones lineales se interseca en un punto (solución única) o en un infinito número de puntos (infinito número de soluciones), el sistema se conoce como consistente.
Cuando un sistema de ecuaciones lineales no se interseca en ningún punto (no existe solución), el sistema se conoce como inconsistente.