Hinreichende Bedingung für Hoch-,Tief- und Wendepunkte

Author:Teacher Weitkamp, Thorsten Heinzler

Topic:Curve Sketching, Derivative, Differential Calculus, Functions, Polynomial Functions

Differentialrechnung Wendepunkte Bergsteiger

Bediene den Schieberegler. Blende die Ableitungen ein (Check-Box) Der Verlauf des Höhenprofils ist zum Teil linkskrümmig und zum Teil rechtskrümmig. Notiere die Stelle auf der x-Achse des steilsten Anstieg. Welche Aussagen sind für die 1.Ableitung und die 2. Ableitung korrekt?

Select all that apply

A
f'(x) hat an der Stelle eine Nullstelle, f''(x) hat eine Maximalstelle
B
f'(x) hat an der Stelle eine Minimalstelle, f''(x) hat eine Nullstelle
C
f'(x) hat an der Stelle eine Maximalstelle, f''(x) hat eine Nullstelle

Check my answer (3)

Der Wanderer erreicht den lokalen Hochpunkt seiner Wanderung. Notiere die Stelle auf der x-Achse. Blende die 1.Ableitung und die 2.Ableitung ein. Welche Aussagen sind korrekt.

Select all that apply

A
f'(x) hat an der Stelle ein Nullstelle; f''(x) hat an der Stelle ein negatives Vorzeichen.
B
f'(x) hat an der Stelle ein Nullstelle; f''(x) hat an der Stelle ein positives Vorzeichen.
C
f'(x) hat an der Stelle ein Maximalstelle; f''(x) hat an der Stelle eine Nullstelle.

Check my answer (3)

Der Wanderer hat auf seiner Wanderung einen lokalen Tiefpunkt durchschritten. Notiere die zugehörige x-Stelle auf der x-Achse. Welche Aussagen sind korrekt?

Select all that apply

A
f'(x) hat an der Stelle eine Nullstelle; f''(x) hat ein negatives Vorzeichen
B
f'(x) hat an der Stelle eine Nullstelle; f''(x) hat ein positives Vorzeichen
C
f'(x) hat an der Stelle eine Minimalstelle; f''(x) hat ein positives Vorzeichen

Check my answer (3)

Hinreichende (nicht notwendige) Bedingung für Hoch-Tief- und Wendepunkte

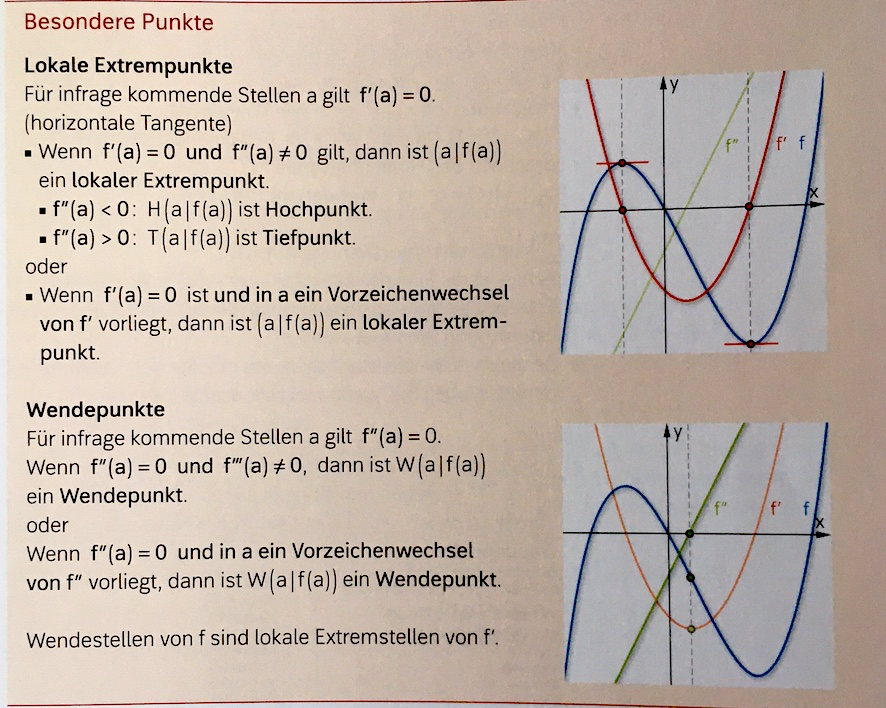
Verständnisfrage 1

Für eine Funktion g(t) gilt: g'(1)=0 und g''(1)=8. Die Stelle t=1 ist ..... Hilfestellung: Die Stelle t=1 liegt im Bereich, in dem die Funktion linkskrümmig ist

Select all that apply

A
eine Wendestelle
B
eine Maximalstelle
C
eine Minimalstelle
D
weder noch

Check my answer (3)

Verständnisfrage 2

Für eine Funktion g(t) gilt: g'(-2)=0 und g''(-2)=-6,5. Die Stelle t=-2 ist ..... Hilfestellung: Die Stelle t=-2 liegt im Bereich, in dem die Funktion rechtskrümmig ist

Select all that apply

A
eine Wendestelle
B
eine Maximalstelle
C
eine Minimalstelle
D
weder noch

Check my answer (3)

Verständnisfrage 3

Für eine Funktion h(r) gilt: h'(10)=0 und h''(10)=0,12. Die Stelle r=10 ist ..... Hilfestellung: Die Stelle r=10 liegt im Bereich, in dem die Funktion linkskrümmig ist

Select all that apply

A
eine Wendestelle
B
eine Maximalstelle
C
eine Minimalstelle
D
weder noch

Check my answer (3)

Verständnisfrage 4

Für eine Funktion f(s) gilt: f'(0)=1 und die Stelle s=0 ist eine Maximalstelle für f'(s).....

Select all that apply

A
eine Wendestelle
B
eine Maximalstelle
C
eine Minimalstelle
D
weder noch

Check my answer (3)

Verständnisfrage 5

Für eine Funktion h(t) gilt: h'(5)=0 und die Stelle t=5 ist eine Minimalstelle für h' . Die Stelle t=5 ist .....

Select all that apply

A
eine Wendestelle
B
eine Maximalstelle
C
eine Minimalstelle
D
Sattelstelle

Check my answer (3)

Verständnisfrage 6

Für eine Funktion h(t) gilt: h'(5)=0 und h''(5)=0 und h'''(5)=2 Die Stelle t=5 ist .....

Select all that apply

A
eine Wendestelle
B
eine Maximalstelle
C
eine Minimalstelle
D
kann so nicht beantwortet werden

Check my answer (3)

Versuche es nun selbst! Bestimme die Extremstellen der Funktion f(x)=-x²+2x mit dem Hinreichenden Kriterium: a) ermittle die 1.Ableitung und ihre Nullstellen b) Ermittle die 2.Ableitung und prüfe das Vorzeichen der 2.Ableitung an den Nullstellen der 1.Ableitung. Denk dran! Wenn das Vorzeichen f''(x) an der Nullstelle von f'(x) negativ ist, so liegt eine Maximalstelle vor. Wenn das Vorzeichen f''(x) an der Nullstelle von f'(x) positiv ist, so liegt eine Minimalstelle vor. Schreibe dein Vorgehen auf! Lösung: x=1 ist Maximalstelle

Hinreichende Bedingung für Hoch-,Tief- und Wendepunkte

Differentialrechnung Wendepunkte Bergsteiger

Hinreichende (nicht notwendige) Bedingung für Hoch-Tief- und Wendepunkte

Verständnisfrage 1

Verständnisfrage 2

Verständnisfrage 3

Verständnisfrage 4

Verständnisfrage 5

Verständnisfrage 6

New Resources

Discover Resources

Discover Topics