Conjunto Solución de una Ecuación Lineal en ℝ² (pareja ordenada)
Una solución de una ecuación lineal en variables es una sucesión de números reales ordenados de modo que la ecuación se cumple cuando los valores se sustituyen en ésta.
Por ejemplo, la ecuación . Se cumple cuando y . Otras soluciones son y, y también y .
El conjunto de todas las soluciones de la ecuación lineal se denomina Conjunto Solución y cuando se determina este conjunto, se dice que se ha resuelto la ecuación. Para describir todo el conjunto solución de una ecuación lineal, a menudo se utiliza la representación paramétrica.
Ejemplo:
Resuelva la ecuación lineal
Para resolver la ecuación despejamos una de las variables y la dejamos en función de la segunda variable:
De esta manera es una variable libre, lo cual significa que puede tomar cualquier valor real. La variable no es libre, ya que su valor dependerá del valor asignado a . Para representar un número infinito de soluciones de esta ecuación es conveniente introducir una tercera variable denominada parámetro. Así, con , se puede representar el conjunto solución como:
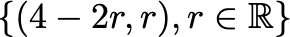
Para obtener soluciones particulares debemos asignar valores al parámetro , por ejemplo:
Entonces sustituyendo en la expresión la solución particular es la pareja ordenada
Actividad:
Captura los coeficientes numéricos del conjunto solución en el applet de la siguiente manera:
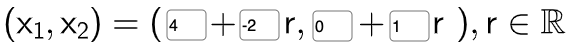
Ahora puedes seleccionar la opción "Mostrar Conjunto Solución", esto permite observar la representación geométrica del Conjunto Solución de la Ecuación Lineal.
Ahora, selecciona la opción "Soluciones Particulares", esta opción permite graficar una pareja ordenada como solución particular, por ejemplo cuando

Cuando captures los coeficientes numéricos de la solución particular anterior se observará que el Punto pertenece al conjunto solución y por lo tanto se encuentra sobre la recta.
Actividad:
Proporciona tres soluciones particulares de la forma (x, y) de la recta