第二节 决策树的构建
一、ID3算法
ID3算法的核心是在决策树各个结点上对应信息增益准则选择特征，递归地构建决策树。
具体方法是：
第一步。从根结点（root node）开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征。
第二步。由该特征的不同取值建立子节点，再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止；
第三步。最后得到一个决策树。
依然以打球数据集为例。由以上计算可知：
，即数据集的总信息熵为0.9403。
，即在确定的情况下，数据集的信息熵已降低为0.6935。则信息增益为 ，同理，可计算其他特征分量的信息增益值为：
,
则根据以上计算，特征的信息增益值最大，为0.2468，按照决策树ID3算法的第一步，所以选特征为根节点。画图（图3-1）可表示如下：
图3-1 根节点
共有三个取值，分别为(阴天）(晴天）、和(刮风）。按照决策树ID3算法的第二步，我们进一步计算以上三个子特征条件下的信息增益。
在取值条件下，数据集的数据子集已在上节列示，其条件熵为0，代表无随机性，确定性很强，信息增益也为0，根据第二步所说明的判断条件，分枝即停止。
在取值条件下，依据上节计算，数据集的数据子集的信息熵为。进一步计算其他特征值的信息增益可列表如下：
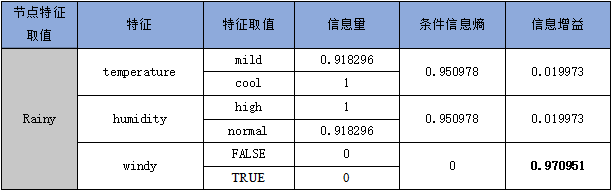
同样，在取值条件下，依据上节计算，数据集的数据子集的信息熵为。进一步计算其他特征值的信息增益可列表如下：
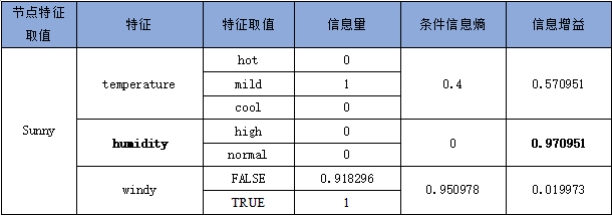
依据以上计算，按照决策树ID3算法的第二步，可以从根节点分枝。画图（图3-2）可表示如下：
图3-2 决策树第二分枝
由以上图可以看出，在第二层分枝中，，分枝停止。而其余两个节点还需要继续分枝，则继续罗列子数据集及如下：
![[justify] [/justify]](https://www.geogebra.org/resource/myv5agt8/6HOgNv0nfq3cBE1G/material-myv5agt8.png)
由以上两表可以快速计算出、，同时，、。由此第三层分枝也全部停止，可以画出天气与打球关系的全貌决策树如图3-3所示：
图3-3 天气-打球决策树
根据以上决策树，可以形成对是否打球的基本判断逻辑是：首先看天气状况，如果是阴天，则去打球；如果是雨天，则看是否刮风，如刮风，则不去打球，如不刮风，则去打球；如果是晴天，则看湿度状况，如果高，则不去打球，如果正常，则去打球。
二、C4.5算法
与ID3算法相似，但是做了改进，将信息增益率作为选择特征的标准。
信息增益率=信息增益/属性熵。用公式表示为：
(有问题）
其中，个值。若使用来对样本集进行划分，则会产生个分枝节点，其中第个节点包含中所有属性上取值为的样本，记为。通常，属性的可能取值数越多（即越大），则的值通常会越大。
具体方法是：
输入：训练数据集，特征集，阈值；
输出：决策树。
（1）如果中所有实例属于同一类，或，则设置为单结点树，并将作为该结点的类，返回；
（2）按公式计算中各特征对的信息增益比，选择信息增益比最大的特征；
（3）如果的信息增益比小于阈值，则设置为单结点树，并将中实例数最大的类作为该结点的类，返回；
（4）否则，对的每一可能值，依将分割为若干非空子集，并将中为特征集，递归地调用步（1）～步（4），得到子树
，返回
。实例数最大的类作为标记，构建子结点，由结点及其子结点构成树，返回；
（5）对结点，以为训练集，以A→﹛A﹜为特征集，递归地调用步（1）～步（4），得到子树，返回。
，返回。实例数最大的类作为标记，构建子结点，由结点及其子结点构成树，返回；
（5）对结点，以为训练集，以A→﹛A﹜为特征集，递归地调用步（1）～步（4），得到子树，返回。 同样以天气打球数据集为例，根据此前计算，数据集的经验熵。而各特征变量的属性熵为：
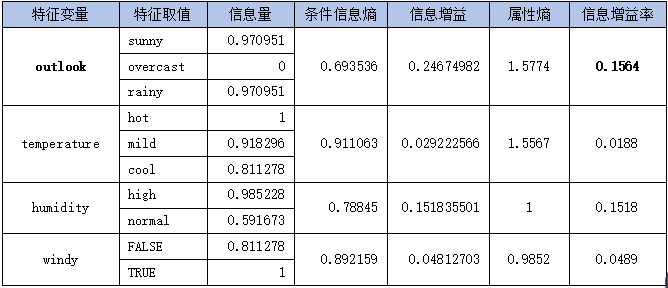
则根据以上计算，依然是特征的信息增益率最大，为0.1564，按照决策树C4.5算法的第三和第四步，依然选特征为根节点。并由此可进一步计算各特征值的信息增益率并列表如下：
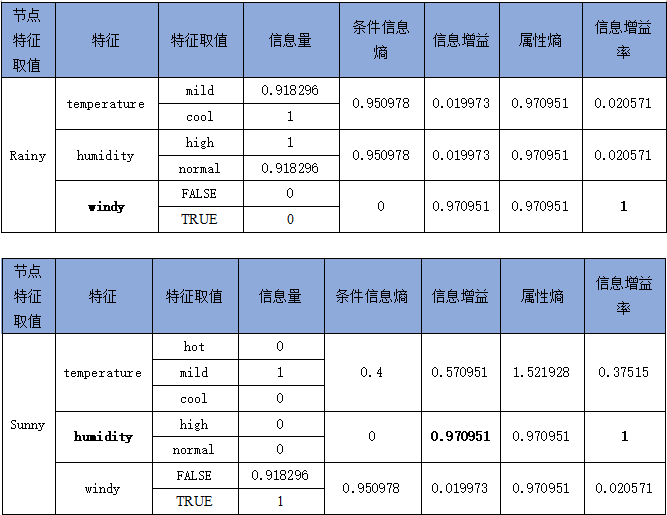
至此，第二层分枝已全部确定，按照C4.5的具体执行步骤，可以很快看出，还需要向下分枝第三层。请同学们自行计算并画出一幅完整的决策树图。
以上所有的计算过程及步骤均在右侧的二维码中详细列明，请读者扫描并下载为本地文件，即可查看。
现在的问题是，信息增益的方法（ID3）已经可以选出划分属性了，为什么还要有信息增益率算法（C4.5）。因为信息增益方法是有缺陷的。主要缺陷为：如果各个特征变量的值的个数比较平均，比如都是2～3个值，缺陷就不明显；而如果各个特征变量的值的个数差异较大，会发现信息增益偏向值个数多的属性。所以为了纠正这个缺陷，C4.5 决策树提出了信息增益率。对于增益率分母越大值越小，所以信息增益率可以起到“惩罚”值个数多的属性的目的。但是如果算法全部使用信息增益率，又会出现偏向值个数少的属性这一缺陷，所以 C4.5其实并没有直接使用信息增益率，而是先用信息增益选出一些高于平均水平的属性候选集，再从候选集中选出信息增益率最高的属性，也算是一种折中。
C4.5算法还可以将连续的属性进行离散化，离散化策略就是二分法，在此不赘述，请感兴趣的同学自行查阅相关资料。
在决策树经典算法中，除了ID3和C4.5之外，还有一种CART算法，CART决策树采用基尼系数选取最优划分属性。基尼系数的公式为，可以看出，基尼系数反映了随机抽取两个样本，其类别不一致的概率。基尼系数反映的是分支内任意两个样本分类不一致的情况，所以基尼系数越小，分类越纯，所以我们选取基尼系数最小的属性作为最优划分属性。
三、ID3、C4.5、CART的区别算法
对于这三个非常著名的决策树算法，简单地区别是：ID3使用信息增益作为选择特征的准则；C4.5使用信息增益率作为选择特征的准则；CART使用基尼系数作为选择特征的准则。
ID3：熵表示的是数据中包含的信息量大小。熵越小，数据的纯度越高，也就是说数据越趋于一致，这是我们希望的划分之后每个子节点的样子。
信息增益=划分前熵-划分后熵。信息增益越大，则意味着使用属性
来进行划分所获得的“纯度提升”越大。也就是说，用属性
来划分训练集，得到的结果中纯度比较高。
ID3仅仅适用于二分类问题；ID3也仅仅能够处理离散属性。
C4.5：克服了ID3仅仅能够处理离散属性的问题，以及信息增益偏向选择取值较多特征的问题，使用信息增益率来选择特征。信息增益率=信息增益/属性熵，选择信息增益率最大的作为最优特征。
C4.5处理连续特征是先将特征取值排序，以连续两个值中间值作为划分标准。尝试每一种划分，并计算修正后的信息增益，选择信息增益最大的分裂点作为该属性的分裂点。
CART：与ID3、C4.5不同之处在于CART生成的树必须是二叉树。也就是说，无论是回归还是分类问题，无论特征是离散的还是连续的，无论属性取值有多个还是两个，内部节点只能根据属性值进行二分。
CART的全称是分类与回归树。从这个名字中就应该知道，CART既可以用于分类问题，也可以用于回归问题。
回归树中，使用平方误差最小化准则来选择特征并进行划分。每一个叶子节点给出的预测值，是划分到该叶子节点的所有样本目标值的均值，这样只是在给定划分的情况下最小化了平方误差。
要确定最优化分，还需要遍历所有属性，以及其所有的取值来分别尝试划分并计算在此种划分情况下的最小平方误差，选取最小的作为此次划分的依据。由于回归树生成使用平方误差最小化准则，所以又叫做最小二乘回归树。
来进行划分所获得的“纯度提升”越大。也就是说，用属性来划分训练集，得到的结果中纯度比较高。
ID3仅仅适用于二分类问题；ID3也仅仅能够处理离散属性。
C4.5：克服了ID3仅仅能够处理离散属性的问题，以及信息增益偏向选择取值较多特征的问题，使用信息增益率来选择特征。信息增益率=信息增益/属性熵，选择信息增益率最大的作为最优特征。
C4.5处理连续特征是先将特征取值排序，以连续两个值中间值作为划分标准。尝试每一种划分，并计算修正后的信息增益，选择信息增益最大的分裂点作为该属性的分裂点。
CART：与ID3、C4.5不同之处在于CART生成的树必须是二叉树。也就是说，无论是回归还是分类问题，无论特征是离散的还是连续的，无论属性取值有多个还是两个，内部节点只能根据属性值进行二分。
CART的全称是分类与回归树。从这个名字中就应该知道，CART既可以用于分类问题，也可以用于回归问题。
回归树中，使用平方误差最小化准则来选择特征并进行划分。每一个叶子节点给出的预测值，是划分到该叶子节点的所有样本目标值的均值，这样只是在给定划分的情况下最小化了平方误差。
要确定最优化分，还需要遍历所有属性，以及其所有的取值来分别尝试划分并计算在此种划分情况下的最小平方误差，选取最小的作为此次划分的依据。由于回归树生成使用平方误差最小化准则，所以又叫做最小二乘回归树。