Teorema de Pick
Actividad 1. Observa los siguientes polígonos, cuyos vértices tienen coordenadas enteras.
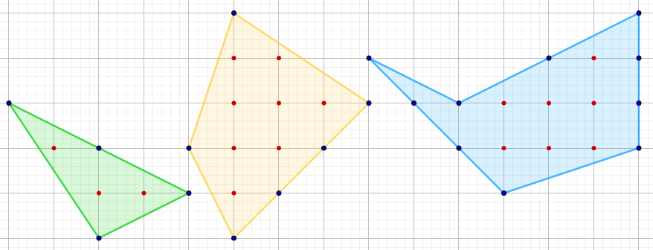
Construye estos u otros similares con GeoGebra y calcula sus áreas, mediante el comando 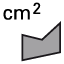 .
.
 .
.Ahora, rellena la siguiente tabla, donde B = nº de puntos con coordenadas enteras en el borde (puntos azules), e I = nº de puntos con coordenadas enteras en el interior del polígono (puntos rojos). ¿Qué observas?
¿Cuál intuyes que será la fórmula para hallar el área de cualquier polígono con vértices de coordenadas enteras? Este resultado se conoce como el teorema de Pick.
| | I | B | I+B/2-1 | Área |
| Triángulo | ||||
| Cuadrilátero | | | | |
| Pentágono | | | | |