7. Obtención de ecuaciones en una recta
Ecuacion de una recta dada un punto y una recta paralela
Para hallar la ecuación de una recta, se necesita tener el punto de paso y el "vector de dirección",
se nos puede proporcionar un punto y la ecuación de otra recta la cual tiene que ser paralela a la que estamos trabajando
P=(x,y,z)
La ecuación de la recta paralela la podemos encontrar de manera simétrica o paramétrica
La ecuación paramétrica se entiende como:
x= + at
y= + bt
z= + ct
Mientras que la ecuación paramétrica se comprende como:
El vector director se puede encontrar usando la ecuación de la recta paralela que se ha proporcionado, pues al ser paralela a la ecuación que queremos encontrar, el vector dirección será el mismo.
El vector director se entiende como =(a,b,c),
Para construir la ecuacion de la recta, se tiene que hacer la ecuación victoria:
S: (x,y,z) = P + ()
Mientras que la ecuación paramétrica se comprende como:
El vector director se puede encontrar usando la ecuación de la recta paralela que se ha proporcionado, pues al ser paralela a la ecuación que queremos encontrar, el vector dirección será el mismo.
El vector director se entiende como =(a,b,c),
Para construir la ecuacion de la recta, se tiene que hacer la ecuación victoria:
S: (x,y,z) = P + ()
Hallar la ecuacion de la recta que pasa por el punto P=(5,3,-7) y es paralela a la recta r:
Ecuación de una recta dada un punto y una recta perpendicular
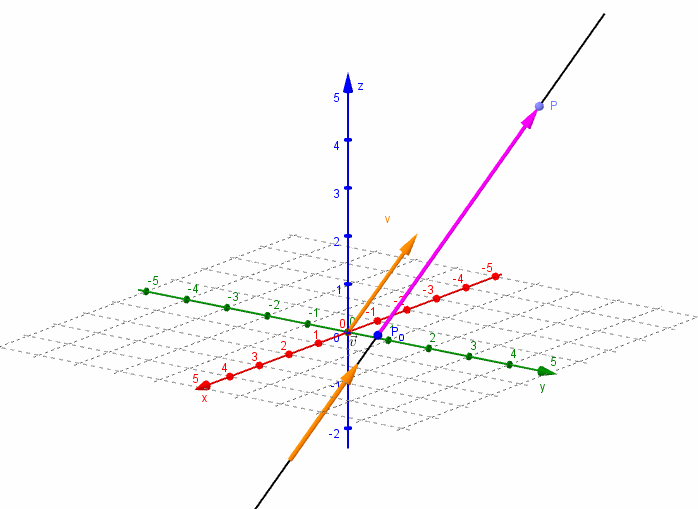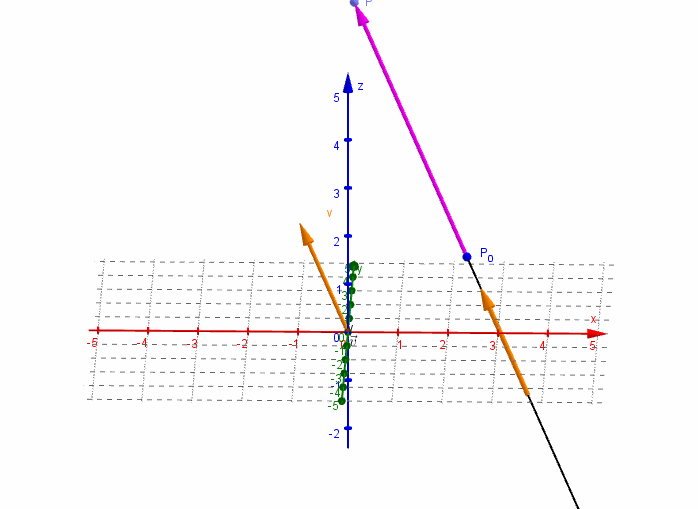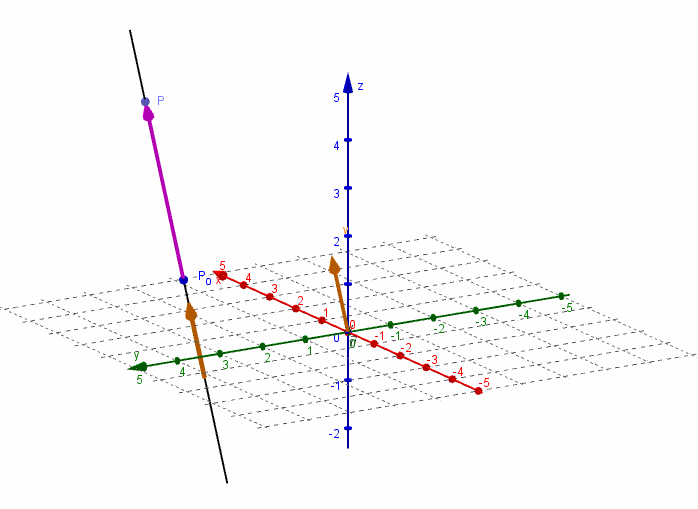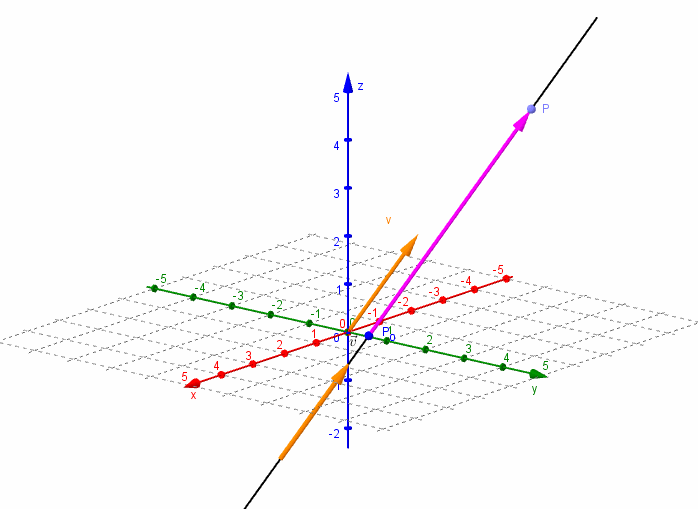
En el espacio R3, un vector se expresa como:
v= (a, b, c) por lo que, de manera similar a la región R2, podríamos realizar la deducción de las ecuaciones paramétricas de la recta en el espacio.
Resultando en la siguiente definición:
Ecuaciones paramétricas y simétricas de la recta en el espacio
Sea P(X1, Y1, Z3) un punto en el espacio que además está sobre una recta L y sea v=(a, b y c) el vector de dirección en R3 para la recta.
Rectas perpendiculares
Autores
Miranda Valtierra Luis Angel
Ruiz García Abril
Ulises Castañeda Zuñiga
Gaddard Talavera Josué Alan