Diferenciación a través de diferencias divididas





Ejemplo
Use aproximaciones con diferencias finitas hacia adelante y hacia atrás de O(h) y una aproximación de diferencias centradas de O(h2) para estimar la primera derivada de
en x = 0.5 utilizando un incremento de h = 0.5. Repita el cálculo con h = 0.25. Observe que la derivada
se calcula directamente como
y se puede utilizar para calcular el valor verdadero como f ′(0.5) = –0.9125.
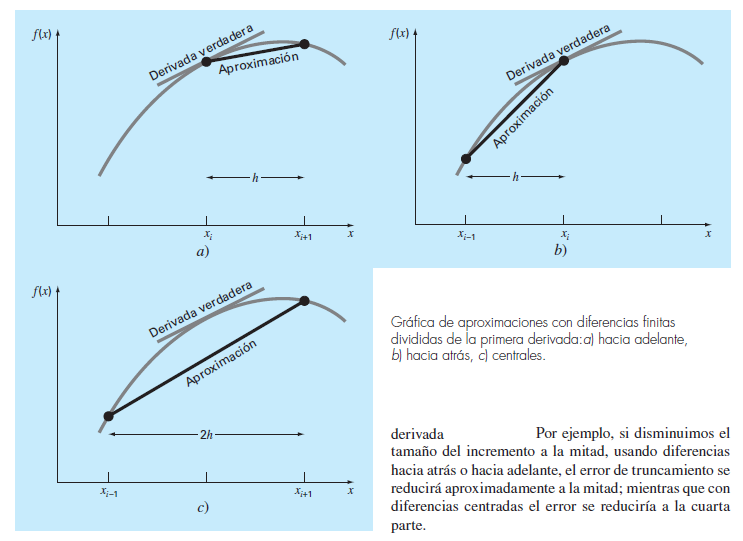
Para ambos tamaños de paso, la aproximación en diferencias centrales es más exacta que las diferencias hacia adelante y hacia atrás. También, como se pronosticó con el análisis de la serie de Taylor, dividiendo a la mitad el incremento, se tiene aproximadamente la mitad del error en las diferencias hacia atrás y hacia adelante y una cuarta parte de error en las diferencias centradas.