Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

LEMBAR KERJA PESERTA DIDIK 2 DIMENSI TIGA

Author:Reka Kirana
Image

Petunjuk Penggunaan

1. Isikan identitas dengan benar pada bagian yang telah tersedia. 2. Jika diperlukan, silahkan putar video pembahasan mengenai materi jarak titik ke garis. 3. Kerjakan aktivitas bersama kelompok masing-masing secara runtut dan seksama.

Tujuan Pembelajaran

1. Siswa mampu menentukan jarak antara titik terhadap garis dalam ruang dimensi tiga. 2. Siswa mampu menganalisis jarak antara titik terhadap garis dalam ruang dimensi tiga.

Identitas Kelompok

Pilih salah satu sesuai dengan pembagian kelompok

Select all that apply
  • A
  • B
  • C
  • D
  • E
  • F

Isikan identitas anggota kelompok (nama, nomor presensi)

Mari Mengingat

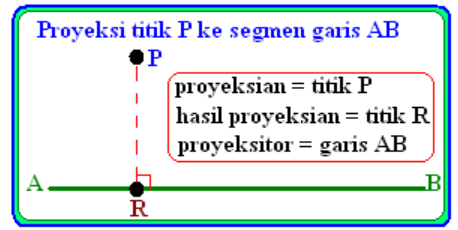
1. Proyeksi Titik ke Garis

Proyeksi sebuah titik P pada sebuah garis g dapat diperoleh dengan menarik garis tegak lurus dari titik P terhadap garis g. Proyeksi ini menghasilkan sebuah titik P' yang disebut titik proyeksi.
sumber: blog.koma
sumber: blog.koma

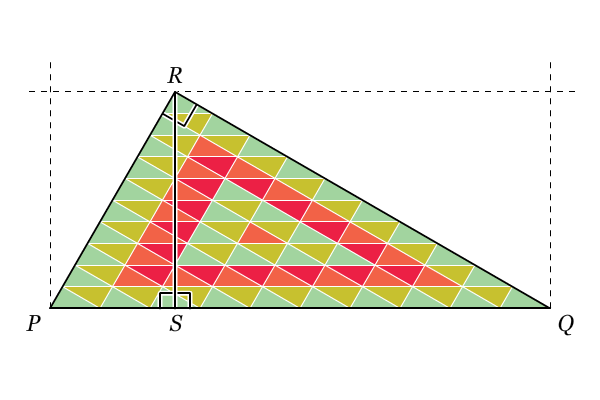
2. Kesebangunan pada Segitiga Siku-Siku

Konsep dari alas dan tinggi segitiga merupakan kedua sisi segitiga yang tegak lurus satu sama lain. Sehingga untuk perhitungan luas segitiga dapat menggunakan sisi manapun asalkan keduanya tegak lurus satu sama lain.
sumber: Grasindo Publisher
sumber: Grasindo Publisher

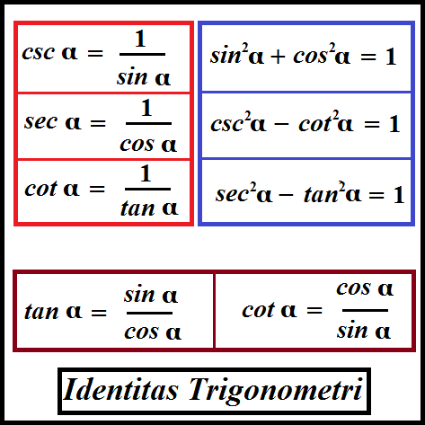
3. Identitas Trigonometri

3. Identitas Trigonometri
sumber: Anto Tunggal

Mari Memahami

Materi jarak titik ke garis

Definisi Jarak Titik ke Garis

Jarak titik ke garis merupakan ruas garis tegak lurus atau terpendek dari sebuah titik terhadap sebuah garis. Dengan definisi lain, jarak titik ke garis merupakan hasil proyeksi dari titik ke garis.

Ilustrasi

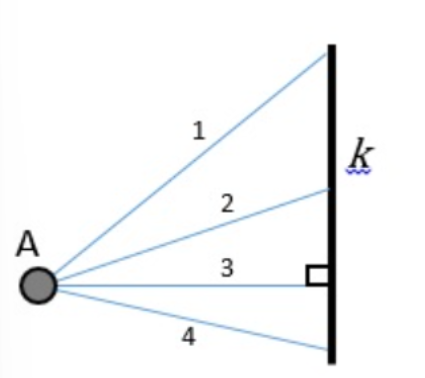
Ilustrasi
sumber: Haloedukasi.com

Manakah yang merupakan jarak antara titik A dengan garis k?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Diskusikan bersama kelompokmu alasan memilih jalur tersebut

Mari Berlatih

Coba kerjakan aktivitas berikut dengan seksama

Panjang rusuk kubus ABCD.EFGH adalah 5 cm. Jarak titik G ke diagonal HB adalah ... cm
Bentuk suatu bidang untuk mempermudah mencari jarak antara titik G dengan garis HB.
Jika iya, maka kita dapat mencari jarak titik G ke garis HB menggunakan kesebangunan segitiga (lihat bagian "mari mengingat" nomor 2)

Diskusikan bersama kelompokmu, apakah segitiga BGH merupakan segitiga siku-siku?

Select all that apply
  • A
  • B
Check my answer (3)

Berapa panjang jarak titik G ke garis HB yang kelompok kalian peroleh?

1. Gambarkan apa yang diminta oleh soal

Mari Mencoba Lebih Dalam

Masih dengan kubus yang sama, diskusikan bersama kelompok masing-masing.

Bidang apa yang kalian ambil untuk mencari jarak titik A ke titik G?

Berapa panjang jarak titik A ke titik G?

Cara mana yang kelompok kalian pilih?

Select all that apply
  • A
  • B

New Resources

Discover Resources