Welches Rechteck ist am größten?
Grundproblem
Gesucht ist das größte achsenparallele Rechteck im ersten Quadranten unter der Geraden mit der Gleichung .
Mit dynamischer Geometrie experimentieren
Nähere dich der Lösung zunächst durch Probieren. Verwende dabei das Applet "Rechtecksuche".
Ermittle das größtmögliche Rechteck systematisch.
Wertetabelle
Ermittle für verschiedene Längen der Grundseite den Flächeninhalt der Rechtecks. Du erhälst eine Wertetabelle, so dass du den zugehörigen Graph zeichnen kannst.
Überprüfe dein Ergebnis beim "Check".
Wie groß ist der Flächeninhalt des flächengrößten Rechtecks?
Von der Vermutung zur Begründung
Begründe, dass das von dir gefundene größte Rechteck wirklich das größtmögliche ist.
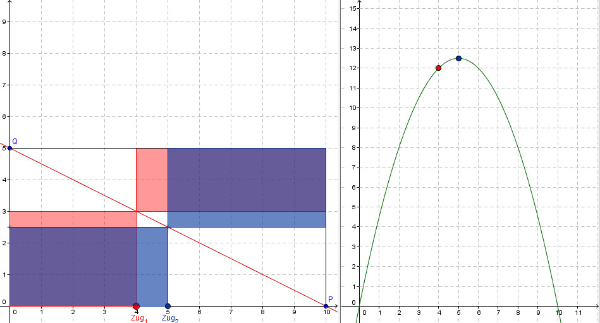
Von der Wertetabelle zum Graphen
Ermittle für verschiedene Längen der Grundseite den Flächeninhalt der Rechtecks.
Von der Wertetabelle zum Graphen
Erstelle den zur obigen Wertetabelle gehörenden Graphen. Der Graph gibt dann den Flächeninhalt des Rechtecks in Abhämgigkeit von der Länge der Grundseite an. Beispielsweise ist (0,6|2,7) ein Punkt des Graphen, weil das Rechteck mit einer Grundseite der Länge 0,6 LE genau 4,5 LE hoch ist und daher einen Flächeninhalt von 0,6 LE * 4,5 LE = 2,7 FE hat.
Für schlaue Füchse
Gelingt es dir, den Funktionsterm des Graphen anzugeben?