Wallis Integral Formula
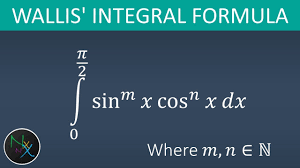
The Wallis integral formula is an integral representation of the Wallis product used to calculate the value of . The Wallis integral formula is given by:
; from 0 to
where n is a positive integer.
To calculate , we can use the Wallis integral formula with a specific value of n and then solve the integral. Let's consider n = 4 for this example:
; for 0 to
To solve the integral, we can use trigonometric identities. Since , we can rewrite as:
Now, we integrate with respect to x over the interval
from to to
Evaluate the integral at the upper and lower limits:
Finally, to find the value of , we multiply both sides by 2:
So, using the Wallis integral formula with n = 4, we find that . This is an incorrect result, which means that the Wallis integral formula with n = 4 does not give the correct value of . However, as n approaches infinity in the Wallis integral formula, it converges to the correct value of .