Die Quadratwurzel
Technische Voraussetzungen
Für das Kapitel quadratische Funktionen benötigen Sie einen Taschenrechner.
Die Schule benutzt einen TI - 30X, ein sehr altes Modell. Ich benutze für meine Fotos die Software für den TI 30 - XS Multiview. Sie müssen sich keinen Rechner von Texas Instruments (TI) kaufen, aber Sie müssen versuchen mit IHREM Taschenrechner (TR) zurechtzukommen. Ein Handy geht zur Not auch, - zu Hause, oder im Unterricht- nicht jedoch für Klassenarbeiten und schon gar nicht in der ZP 10.
In der Regel sind die Erklärungen zum Gebrauch IHRES Taschenrechners ausreichend.
Von der Fläche (Umfang) zur Seitenlänge
In dem vorigen Abschnitt haben Sie erkannt, dass sich die Fläche eines Quadrates anders entwickelt als der Umfang, aber beides ist von derselben Größe abhängig, der Seitenlänge (a) des Quadrates.
Deshalb können Sie auch nicht mit Ihren bisherigen mathematischen Kenntnissen von der Fläche auf die Seitenlänge schließen. Das folgende Arbeitsblatt hilft Ihnen, das Werkzeug des Wurzel Ziehens zu erkunden und zu verstehen.
02_Quadratwurzel
Die Tastenfolge zur Berechnung der Quadratwurzel
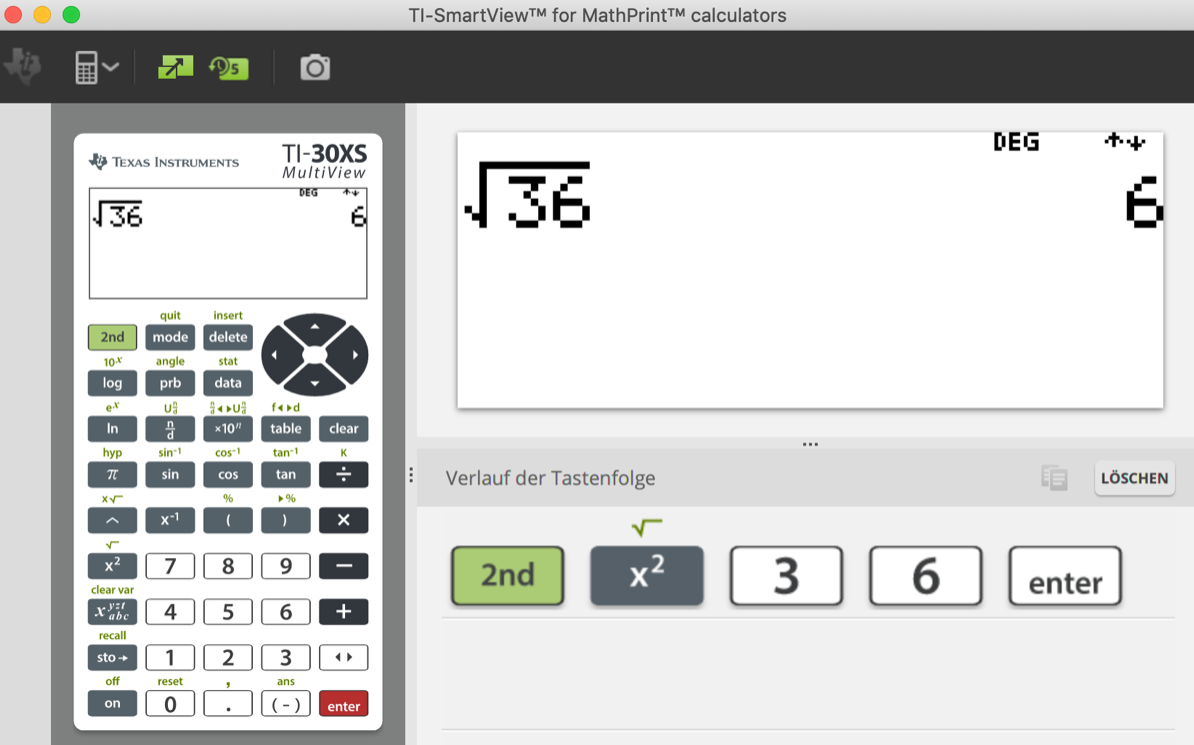
Lösungsblatt zur Quaderatwurzel
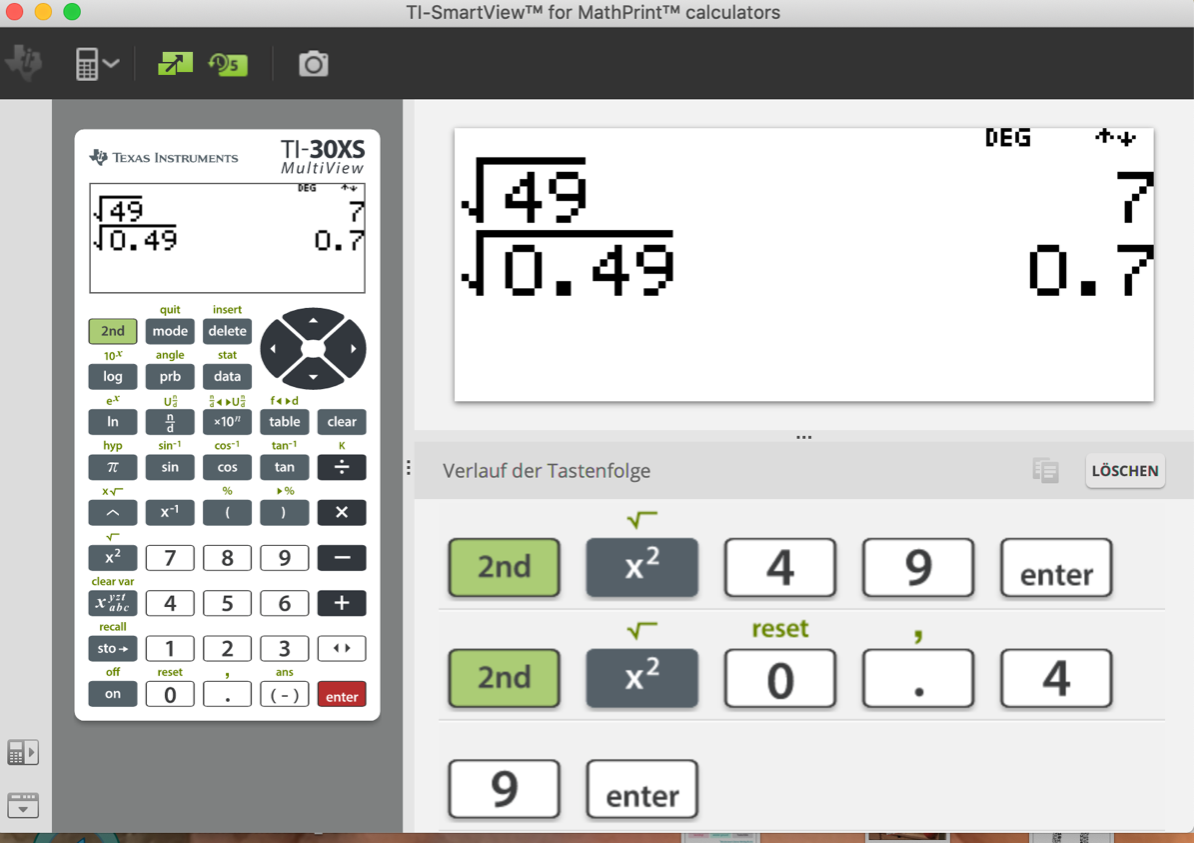
Quadratwurzel aus 49 und 0.49
Quadratzahlen
Unter den natürlichen Zahlen gibt es einige Besonderheiten, von den jetzt gerade zwei interessant sind:
A: Einmal unterscheiden sich die natürlichen Zahlen bei der Division durch 2:
i: es bleibt der Rest 0 (kein Rest) ==> diese Zahlen sind gerade
ii. es bleibt der Rest 1 ==> diese Zahlen sind ungerade.
B:
Es gibt Zahlen, bei denen die Quadratwurzel wieder eine natürliche Zahl ist. Das ist gleichbedeutend damit, dass sie sich als Produkt von zwei gleichen natürlichen Zahlen schreiben lassen.
Da Produkte von Zahlen immer Flächen darstellen, reperäsentieren diese Produkte Quadrate und werden deshalb Quadratzahlen genannt.
Das nachfolgende Applet verdeutlicht diesen Zusammenhang.
Das Wissen über Quadratzahlen erleichtert den Umgang mit quadratischen Gleichungen.
Deshalb ist es empfehlenswert, die Quadratzahlen bis 20 zu kennen, also auswendig zu lernen.