E01 Az euklideszi szerkesztés
![[b][url=https://hu.wikipedia.org/wiki/Eukleid%C3%A9sz_(matematikus)]Alexandriai Eukleidész[/url] [/b] ([url=https://hu.wikipedia.org/wiki/G%C3%B6r%C3%B6g_%C3%A1b%C3%A9c%C3%A9]görög betűkkel[/url]: Εὐκλείδης;
([b]Euklidész)[/b] [url=https://hu.wikipedia.org/wiki/I._e._300]i. e. 300[/url] körül született) görög [url=https://hu.wikipedia.org/wiki/Matematikus]matematikus[/url], akit később [i]a [url=https://hu.wikipedia.org/wiki/Geometria]geometria[/url] atyja[/i]ként is emlegettek.](https://www.geogebra.org/resource/kp3zj5wz/UgbmvR5HCjBEymcc/material-kp3zj5wz.png)
Általában szerkesztésnek nevezzük egy geometriai alakzat előállítását, ahol adottak a geometriai alakzat egyértelmű előállításához szükséges adatok, adott az előállítás egyértelműen meghatározott feltételei, algoritmusa (lépései, és ezek sorrendje), és adottak az algoritmus alkalmazásához szükséges eszközök.
Ezt a meghatározást elfogadva minden GeoGebrával készített rajz előállítása szerkesztésnek tekinthető, ahol a szerkesztés eszközei a GeoGebra rajzoló eszközei. Ez természetesen jóval bővebb eszköztár, mint amit az általános- és a középiskolai matematikaórákon szerkesztésnek szokás nevezni. Azt mondjuk, hogy ott euklideszi szerkesztést végzünk, noha euklideszi szerkesztés feltételei jóval szigorúbbak az iskolai szerkesztési feltételeknél. De akár lehet a szerkesztés eszköze egy bögre - mint sablon -, amit körülrajzolva, elfogadjuk, hogy az így kapott alakzat kör.
Euklideszi szerkesztésnek nevezzük az alábbi feltételeknek eleget tevő síkgeometriai alakzatok előállítását:
A szerkesztés eszközei:
- az egyélű egyenes vonalzó, amely alkalmas bármely két pontra illeszkedő egyenes felvételére (megadására);
- a körző, amely alkalmas bármely két pont körzőnyílásba vételére.
A geometriai alakzat előállítása az alábbi hat művelet (szerkesztési lépés)
véges számú alkalmazásával történhet:
1. Két adott 
pontra illeszkedő egyenes előállítása;
2. Két adott egyenes metszéspontjának az előállítása; 
3. Két adott pont szakaszának (távolságának) a körzőnyílásba vétele, átvitele; (kör sugarának megadása);
4. Adott középpontú, adott sugarú kör előállítása.
5. Két adott kör metszéspontjainak az előállítása.
6. Adott kör és adott egyenes metszéspontjainak az előállítása.
A már előállított geometriai alakzat, (pont, egyenes vagy kör) a szerkesztés további menetében adottnak tekinthető.
Megjegyezzük, hogy az euklideszi szerkesztésnek nincs olyan (elvi) akadálya, hogy a vonalzónk túl rövid két pont egyenesének a felvételéhez. Ugyanígy a körző mindig elegendően nagy. (Épp úgy, mint a GeoGebrában.) Rögzítsük le azt is, hogy az eszközeink tökéletesen működnek (nem pontatlanok),és a ezeket ugyancsak pontosan használjuk. Ezzel kizártuk a gyakorlatban előforduló pontatlanságokat.
A körző a kör "definíciója alapján" rajzol, a vonalzó viszont olyan sablonnak (is) tekinthető, mint a bögre a kör rajzolásához. Ezért lehet fontos az a matematikai tétel, miszerint minden euklideszi szerkesztés, (amelynek pontok a bemenő adatai és a végeredménye is) elvégezhető csak körzővel is.
Másik megjegyzendő dolog, hogy ha egy kör és egyenes, vagy két kör éppen érintő helyzetű, akkor az érintési pont kijelölése nem tekinthető euklideszi szerkesztési lépésnek. (Ellentétben a GeoGebrával, amely ilyen esetben is megadja a közös pontot.)
Példaként - kizárólag az euklideszi lépésekre szorítkozva- oldjuk meg az alábbi két feladatot:
Legyen adott az e=(A,B) egyenes, és egy rá nem illeszkedő P pont.
Szerkesszük meg - minél kevesebb lépésben - a P -re illeszkedő
1. e-re merőleges;
2. e-vel párhuzamos
egyenest.
Ez a - szigorú értelemben vett - euklideszi szerkesztés alkalmazása eléggé nehézkessé tenné a gyakorlati munkát. Ezért gyakorlatilag euklideszi szerkesztésnek tekinthetünk minden olyan szerkesztést, amely visszavezethető a fenti hat lépés véges sokszori alkalmazására.
Nem egyszerű - matematikai - kérdés annak az eldöntése, hogy a GeoGebra által alaphelyzetben felkínált parancs ikonok közül melyik tekinthető euklideszi szerkesztésnek, és melyik nem. Az minden esetre komoly segítség, hogy a fentiek értelmében minden euklideszi szerkesztéssel előállított rajz kizárólag körökből egyenesekből, és a megadott bázispontokon túlmenően ezek metszéspontjaiból állhat.
Nehezebb kérdés annak az igazolása, hogy a megszerkesztett alakzat valóban rendelkezik-e a kívánt tulajdonsággal. Különösen akkor, ha egyéb feltételeket is állítunk magunk elé. Például -mondjuk - nem használhatjuk a sokat emlegetett párhuzamossági axiómát, valamint az ebből következő - például a hasonlóságon alapuló - összefüggéseket. Ezzel a kérdéssel itt foglalkozunk bővebben.
pontra illeszkedő egyenes előállítása;
2. Két adott egyenes metszéspontjának az előállítása;
3. Két adott pont szakaszának (távolságának) a körzőnyílásba vétele, átvitele; (kör sugarának megadása);
4. Adott középpontú, adott sugarú kör előállítása.
5. Két adott kör metszéspontjainak az előállítása.
6. Adott kör és adott egyenes metszéspontjainak az előállítása.
A már előállított geometriai alakzat, (pont, egyenes vagy kör) a szerkesztés további menetében adottnak tekinthető.
Megjegyezzük, hogy az euklideszi szerkesztésnek nincs olyan (elvi) akadálya, hogy a vonalzónk túl rövid két pont egyenesének a felvételéhez. Ugyanígy a körző mindig elegendően nagy. (Épp úgy, mint a GeoGebrában.) Rögzítsük le azt is, hogy az eszközeink tökéletesen működnek (nem pontatlanok),és a ezeket ugyancsak pontosan használjuk. Ezzel kizártuk a gyakorlatban előforduló pontatlanságokat.
A körző a kör "definíciója alapján" rajzol, a vonalzó viszont olyan sablonnak (is) tekinthető, mint a bögre a kör rajzolásához. Ezért lehet fontos az a matematikai tétel, miszerint minden euklideszi szerkesztés, (amelynek pontok a bemenő adatai és a végeredménye is) elvégezhető csak körzővel is.
Másik megjegyzendő dolog, hogy ha egy kör és egyenes, vagy két kör éppen érintő helyzetű, akkor az érintési pont kijelölése nem tekinthető euklideszi szerkesztési lépésnek. (Ellentétben a GeoGebrával, amely ilyen esetben is megadja a közös pontot.)
Példaként - kizárólag az euklideszi lépésekre szorítkozva- oldjuk meg az alábbi két feladatot:
Legyen adott az e=(A,B) egyenes, és egy rá nem illeszkedő P pont.
Szerkesszük meg - minél kevesebb lépésben - a P -re illeszkedő
1. e-re merőleges;
2. e-vel párhuzamos
egyenest.
Ez a - szigorú értelemben vett - euklideszi szerkesztés alkalmazása eléggé nehézkessé tenné a gyakorlati munkát. Ezért gyakorlatilag euklideszi szerkesztésnek tekinthetünk minden olyan szerkesztést, amely visszavezethető a fenti hat lépés véges sokszori alkalmazására.
Nem egyszerű - matematikai - kérdés annak az eldöntése, hogy a GeoGebra által alaphelyzetben felkínált parancs ikonok közül melyik tekinthető euklideszi szerkesztésnek, és melyik nem. Az minden esetre komoly segítség, hogy a fentiek értelmében minden euklideszi szerkesztéssel előállított rajz kizárólag körökből egyenesekből, és a megadott bázispontokon túlmenően ezek metszéspontjaiból állhat.
Nehezebb kérdés annak az igazolása, hogy a megszerkesztett alakzat valóban rendelkezik-e a kívánt tulajdonsággal. Különösen akkor, ha egyéb feltételeket is állítunk magunk elé. Például -mondjuk - nem használhatjuk a sokat emlegetett párhuzamossági axiómát, valamint az ebből következő - például a hasonlóságon alapuló - összefüggéseket. Ezzel a kérdéssel itt foglalkozunk bővebben.Szerkesztési feladatok az euklideszi szerkesztés eszközeivel.
Elsőként mutatunk egy-egy lehetőséget a fenti két feladat megoldására.
- Adott az e=(A,B) egyenes és a rá nem illeszkedő P pont. Euklideszi szerkesztési lépésekkel szerkesszük meg a P-re illeszkedő, e- re merőleges egyenest. Milyen geometriai tételre hivatkozva állítjuk, hogy a szerkesztés helyes?
Merőleges szerkesztése euklideszi lépésekkel.
Belátható, hogy a fenti feladat - 7 lépésből álló -megoldásának a helyességét igazoló állítás nem igényli az euklideszi párhuzamossági axióma kimondását.
Párhuzamos egyenes szerkesztése
- Adott az e=(A,B) egyenes és a rá nem illeszkedő P pont. Minél kevesebb euklideszi szerkesztési lépéssel szerkesszük meg a P-re illeszkedő, e- vel párhuzamos egyenest. Milyen geometriai tételre hivatkozva állítjuk, hogy a szerkesztés helyes?
- ha a sík két egyeneséhez van olyan harmadik, amely mindkettőre merőleges, akkor ez a két egyenes nem metszi egymást.
Ebben a megoldásban 12 elemi szerkesztési lépésre volt szükségünk. Vajon megoldható a feladat ennél kevesebb lépésben?
9 lépéssel sikerült megoldanunk a feladatot.
De vajon ennek a szerkesztésnek a helyessége igazolható-e az euklideszi párhuzamossági axióma kimondása nélkül?
Erre a - meglepően nehéz - kérdésre például itt kaphatunk választ.
Az euklideszi szerkesztés általánosabb értelmezése
Amikor - pl. az iskolai gyakorlatban - euklideszi szerkesztésről beszélünk, a legtöbb esetben nem szorítkozunk a fenti hat lépésre. Azt mondjuk, hogy azok az euklideszi szerkesztéssel megoldható feladatok amelyek visszavezethetők a fenti hat lépésre.
Ennek megfelelően a GeoGebra "használható" parancsainak (ill. ikonjainak) köre is bővíthető:
mértani helyként előállhat olyan ponthalmaz, amely nem szerkesztető. Nem szerkeszthetők általában a kúpszeletek. 
, 
Ki kell hagynunk olyan műveleteket, amelyek megadásához numerikus adatok is kellenek. Ilyen például a centrális nyújtás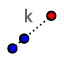 
, adott sugarú kör szerkesztése
, vagy általában szabályos n-szög szerkesztése 
.
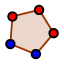A szerkeszthetőség kérdése több mint kétezer éves problémaköre a matematikának. Erre most nem térünk ki. Helyette oldjunk meg ezzel a szűkített eszközkészlettel egy - talán jól ismert - feladatot.
- Pontok::
- Pontokból származtatott egyenes vonalak:
- Vonalakból származtatott egyenesek:
- Körök, körívek:
- Sokszög:
- Transzformációk:
mértani helyként előállhat olyan ponthalmaz, amely nem szerkesztető. Nem szerkeszthetők általában a kúpszeletek. , Ki kell hagynunk olyan műveleteket, amelyek megadásához numerikus adatok is kellenek. Ilyen például a centrális nyújtás , adott sugarú kör szerkesztése , vagy általában szabályos n-szög szerkesztése .
A szerkeszthetőség kérdése több mint kétezer éves problémaköre a matematikának. Erre most nem térünk ki. Helyette oldjunk meg ezzel a szűkített eszközkészlettel egy - talán jól ismert - feladatot. Szabályos ötszög
Feladat:
Legyen adott a sík A ás B pontja. Szerkesszük meg az AB átmérőjű körbe írható szabályos ötszög és szabályos tízszög oldalát!
Egy szerkesztési feladat teljes megoldásának jórészt a probléma elemzéséből, összefüggések kereséséből, majd a szerkesztés lépéseinek a rögzítéséből, magából a szerkesztésből, végül a szerkesztés helyességének az igazolásából kell állnia. Mi most ebből a folyamatból - eléggé el nem ítélhető módon - csak a szerkesztést ragadjuk ki.
Akit kicsit alaposabban érdekelnek e művelet előzményei és következményei, nyúljon vissza a mára megszépült múltba, pl. ide.
Körbe írt szabályos ötszög és tízszög oldala.
A fenti szerkesztést meglapozó két tételt Euklídész így írta le az Elemek XIII. könyvében
EUKLIDÉSZ, Elemek, Gondolat Kiadó, Budapest, 1983, ISBN 963 281 267 0 484.-486. old.):
9. tétel:
"Ha az ugyanabba a körbe írt hatszög és tízszög oldalát összeadjuk, akkor a teljes szakasz folytonos arányban osztott, és a nagyobb darabja a hatszög oldala. "
( A folytonos arány itt az aranymetszés arányát jeleni: )
10. tétel:
"Ha egy körbe egyenlő oldalú ötszöget írunk, akkor az ötszög oldala négyzetértékben egyenlő az ugyanabba a körbe írt hatszög és tízszög oldalának összegével. "
Szerkeszthető, vagy nem?
Amint láttuk, a szabályos ötszög megszerkeszthető az euklideszi szerkesztés eszköztárával. De vajon a szabályos hétszög is megszerkeszthető?
Általában milyen nehéz lehet eldönteni, hogy egy geometriai alakzat euklideszi szerkesztéssel előállítható-e, vagy sem?
A válasz nem túl bízható, bár egyszerű: nehéz!
Így ezzel most nem foglalkozunk.
De itt és itt viszont igen.