Geometria no espaço - Produto escalar
Ângulo formado por dois vetores.
1. Determina a amplitude do ângulo formado pelos dois vetores, com aproximação à décima do grau.
2. Escreve a equação do plano que contém o ponto C e é paralelo ao plano .
Desafio 1: Considera agora que c é um ponto fixo de coordenadas e os pontos A e B são móveis, sendo que e para e . Qual a maior amplitude do ângulo BCA? Desafio-te ainda a replicares esta construção e a indicares a amplitude deste ângulo nessa contrução.
Equação vetorial da reta, no espaço.
3. O ponto de coordenadas pertence à reta ?
4. Escreve uma equação vetorial da reta perpendicular à reta r, que passa no ponto de coordenadas .
Plano tangente à superficie esférica
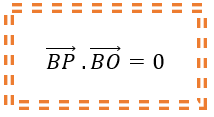
5. Escreve a equação do plano tangente à superficie esférica.
6. Determina as coordenadas dos pontos de interseção deste plano com os eixos.
Equação cartesiana do plano
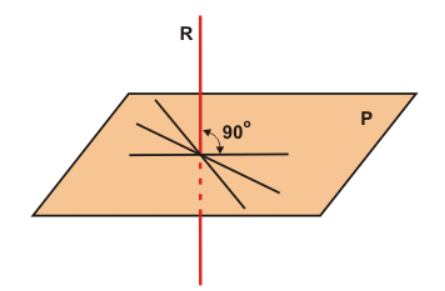
1º caso: dados 3 pontos (não colineares)
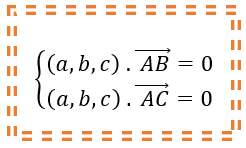
7. Escreve a equação do plano sabendo que, e .