Teorema de Tales

1- Tales e a pirâmide de Quéops.
1.1-Semelhança de triângulos percebida por Tales na pirâmide.
2- O teorema de Tales
O Teorema de Tales pode ser determinado pela seguinte lei de correspondência: “Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes”. Feixe de retas paralelas: Formadas por três ou mais retas de um mesmo plano e que são paralelas entre si. Reta transversal: Reta que corta um feixe de retas paralelas.
3-Explicação e compreensão sobre o Teorema de Tales.
4- Resolvendo e Aprendendo: Utilização do teorema de Tales para calcular a medida desconhecida.

Questão 1- Sabendo que as retas “a”, “b” e “c” são paralelas, calcule o valor de y.

Questão 2-Considere a figura a seguir, na qual a//b//c//.
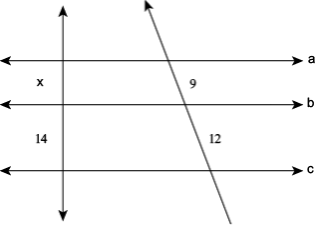
Determine o valor da medida X indicada.
Questão 3

(Saresp–SP) No desenho abaixo estão representados os terrenos I, II e III.Quantos metros de comprimento deverá ter o muro que o proprietário do terreno II construirá para fechar o lado que faz frente com a Rua das Rosas?
Questão 4-De acordo com oque você aprendeu sobre o teorema de Tales, responda a questão a seguir.
Como pode ser definido o Teorema de Tales?
5-Aplicando o teorema de Tales nos triângulos.
Toda paralela a um lado de um triângulo e que encontra os outros dois lados em pontos distintos determina, sobre esses dois lados, segmentos que são proporcionais.
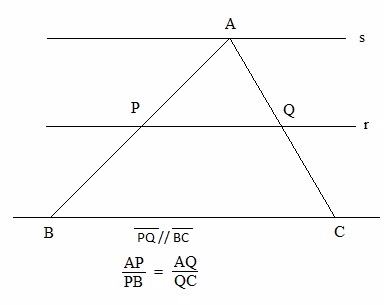
5.1- Aprendendo e aplicando o teorema de Tales em triângulos.
5.2-Resolvendo e Aprendendo: Aplicação do teorema de Tales nos triângulo.

Questão 1-No triângulo ABC a seguir, o segmento DE é paralelo ao segmento BC. Determine o valor de x aplicando a proporcionalidade entre segmentos paralelos cortados por segmentos transversais.
.gif)
Questão 2-Resolva o problema a seguir utilizando teorema de Tales.
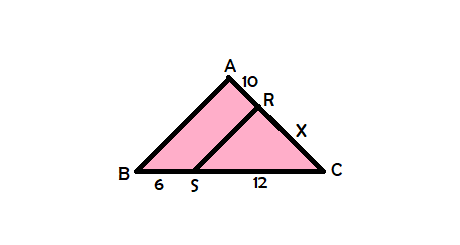
No triângulo ABC, temos que RS//AB. Qual é o valor de X?
Questão 3-Resolva o problema a seguir utilizando teorema de Tales.
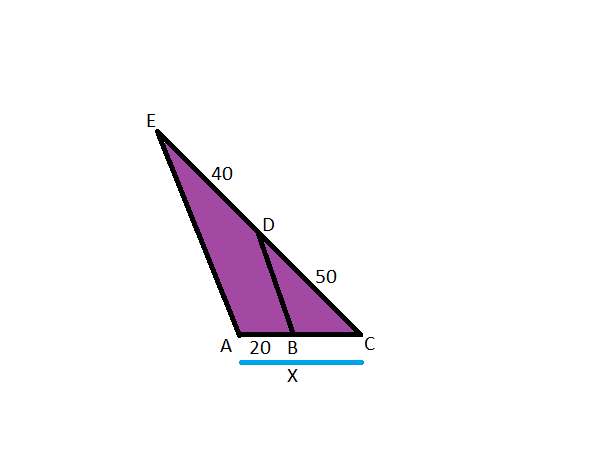
Na figura, BD é paralelo ao lado AE, do triângulo ACE. Determine a medida x indicada e a medida do segmento BC.
Questão 4-Resolva o problema a seguir utilizando teorema de Tales.
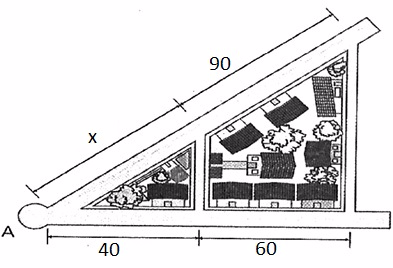
Suponha que a figura ao lado mostre duas avenidas, a e b, que partem de um mesmo ponto A e cortam duas ruas que são paralelas. Em uma das avenidas, is quarteirões determinados pelas ruas paralelas tem 40 m e 60 m de comprimentos. Na outra avenida, um dos quarteirões tem 90 m de comprimento.
6- Situações cotidianas envolvendo teorema de Tales.
6.1-Resolvendo e Aprendendo: Aplicação do teorema de Tales em situações do cotidiano.

Questão 1-Situações do cotidiano.
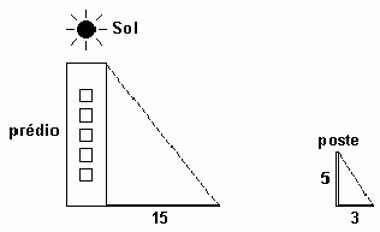
(Unesp) A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:
Questão 2-Situações do cotidiano.
(Fuvest–SP) A sombra de um poste vertical, projetada pelo sol sobre um chão plano, mede 12 m. Nesse mesmo instante a sombra de um bastão vertical de 1 m de altura mede 0,6 m. Qual a altura do poste?