Example of a If-and-Only-If Proof
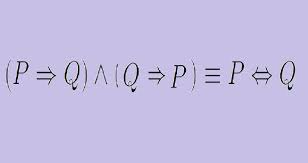
Suppose x ∈ Z. Then x is even if and only if3x+5 is odd.
Proof. We first use direct proof to show that if x is even, then 3x+5 is odd.
If x is even, then x = 2n for some integer n, so 3x+5 = 3(2n)+5 = 6n+5 = 6n+4+1 = 2(3n+2)+1.
Thus 3x+5 is odd because it has form 2k +1, where k = 3n+2 ∈ Z.
Conversely, we need to show that if 3x+5 is odd, then x is even.
We will prove this using contrapositive proof.
Suppose x is not even.
Then x is odd, so x = 2n+1 for some integer n. Thus 3x+5 = 3(2n+1)+5 = 6n+8 =2(3n+4).
This means says 3x+5 is twice the integer 3n+4, so 3x+5 is even, not odd.
Explanation of the Proof:
The proof given is using a combination of direct proof and contrapositive proof to show that x is even if and only if 3x+5 is odd.
A. Direct Proof (if x is even, then 3x+5 is odd):
Assume x is even, which means x = 2n for some integer n.
Substitute x = 2n into the expression 3x+5 and simplify:
3x+5 = 3(2n)+5 = 6n+5 = 6n+4+1 = 2(3n+2)+1.
By expressing 3x+5 in the form 2k+1, where k = 3n+2, we conclude that 3x+5 is odd.
B. Contrapositive Proof (if 3x+5 is odd, then x is even):
Assume the contrapositive, which is that if 3x+5 is odd, then x is not even (i.e., x is odd).
Assume x is odd, which means x = 2n+1 for some integer n.
Substitute x = 2n+1 into the expression 3x+5 and simplify:
3x+5 = 3(2n+1)+5 = 6n+8 = 2(3n+4).
Since 3x+5 is twice the integer 3n+4, we conclude that 3x+5 is even, contradicting the assumption that it is odd. Therefore, by the contrapositive, if 3x+5 is odd, then x must be even.
By proving both the direct implication and the contrapositive implication, the proof establishes the if and only if relationship between x being even and 3x+5 being odd. This means that x is even if and only if 3x+5 is odd, demonstrating the equivalence between the two statements.