Wozu nützt dies?
Konfokale Kurvennetze haben eine enge Beziehung zur komplexen Analysis - zur Funktionentheorie.
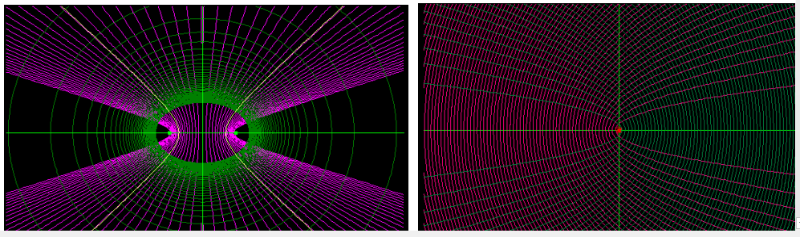
Konfokale Kegelschnitte bilden ein orthogonales Kurvennetz wie die Kurven und einer komplex-differenzierbaren Funktion.
Tatsächlich sind die Kurven und die konfokalen Kegelschnitte zu den Brennpunkten .
Die Funktion ist Lösung der Differentialgleichung .
Die Funktion genügt der Differentialgleichung , die Kurven und sind sind die zur x-Achse symmetrischen, konfokalen Parabeln mit Brennpunkt .
Die Schar der Kegelschnitte, die 4 verschiedene Geraden berühren, besitzen eine interessante Eigenschaft, die sie in die Nähe der obigen Beispiele rückt: Zeichnet man einen der Kegelschnitte als absolute Quadrik aus, so schneiden sich die anderen Quadriken von der absoluten Quadrik aus gesehen, orthogonal.
Wir zeigen dies am Beispiel eines Kreises mit 4 verschiedenen Tangenten.
Man kann die Tangenten und die Berührpunkte symmetrisch zu den Achsen legen. Jeder Punkt im Inneren des Kreises besitzt bezüglich der Symmetrieachsen 3 weitere symmetrisch liegende Punkte (es sei denn, der Punkt liegt auf einer der Symmetrieachsen). Durch die 4 Punkte gehen 2 Kegelschnitte, die aus Symmetriegründen alle 4 Kreistangenten berühren.
Die Kegelschnitt-Tangenten in einem der Kegelschnittpunkte sind Winkelhalbierende der Brennstrahlen, gesehen vom Kreis aus. Daher sind sie "orthogonal".
Das erkennt man auch, wenn man die Pole der beiden Kegelschnitt-Tangenten bezüglich des Kreises untersucht:
der Pol der einen Tangente liegt jeweils auf der anderen Tangente.
Dieses Arbeitsblatt ist Teil des Geogebrabooks Kegelschnitt-Werkzeuge