Ortopirandellianità
“ Le somme e i multipli
sopra di me;
l'ortogonalità dentro di me. „
( parafrasando Kant )
Il teorema di Pitagora ... "sbilenco" !
L'ortogonalità non è un assoluto.
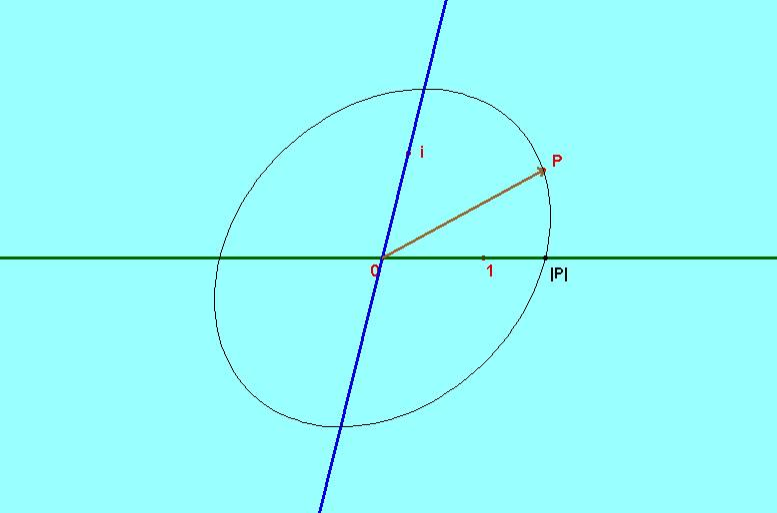
In questa figura la terna (o,u,v) induce la metrica del piano, ossia
fornisce il criterio di "ortogonalità" e la distanza (visualizzata dalla
ellisse dei punti unitari).
Il procedimento di ortogonalizzazione e di metricizzazione indotto dalla scelta di una "base ortonormale"
( ... anche se visivamente "sbilenca" ) :
http://w3.romascuola.net/gspes/0_1_i_modulo.html
Dal punto di vista strutturale, dato un prodotto scalare S in uno spazio vettoriale euclideo E, anche
(a,b) → S(φ(a),φ(b))
è un prodotto scalare in E, per ogni φ automorfismo dello spazio vettoriale E.
Pertanto la "giusta" perpendicolarità è un concetto empirico.
Gli assiomi hilbertiani di congruenza possono descrivere processi di
movimento non corrispondenti a quelli otticamente familiari , una
"Geometria Euclidea Distorta"
( ... Skew Euclidean Geometry, ... o ... Misdisplay Geometry ! ).
Parrebbe esserci una forte riluttanza
a rilasciar gli angoli retti alla balìa
di un ottico ed empirico buon senso!
( vedi Cut the Knot )
L'ellisse unitaria