Subsucesiones
De forma no rigurosa, una subsucesión de la sucesión a(n) es una sucesión que está dentro de la sucesión a(n).
Ejemplo: La sucesión de los números pares es a(n)=2n. Una subsucesión de a(n) es la sucesión de las potencias de dos: b(n) = 2^n.
Los primeros términos de a(n) son
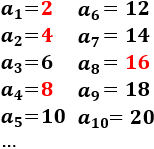 En rojo hemos indicado las potencias de 2, que son los términos de la subsucesión b(n).
Los primeros términos de b(n) son
b(1) = 2 = a(1)
b(2) = 2^2 = 4 = a(2)
b(3) = 2^3 = 8 = a(4)
b(4) = 2^4 = 16 = a(8)
b(5) = 2^5 = 32 = a(16)
...
b(n) = 2^n = a(2^(n-1))
Nota: las subsucesiones de a(n) deben estar compuestas por infinitos términos de a(n). Por ejemplo, la sucesión constante c(n) = 2 = a(1) no es una subsucesión de a(n) porque sólo está formada por un término de a(n).
En rojo hemos indicado las potencias de 2, que son los términos de la subsucesión b(n).
Los primeros términos de b(n) son
b(1) = 2 = a(1)
b(2) = 2^2 = 4 = a(2)
b(3) = 2^3 = 8 = a(4)
b(4) = 2^4 = 16 = a(8)
b(5) = 2^5 = 32 = a(16)
...
b(n) = 2^n = a(2^(n-1))
Nota: las subsucesiones de a(n) deben estar compuestas por infinitos términos de a(n). Por ejemplo, la sucesión constante c(n) = 2 = a(1) no es una subsucesión de a(n) porque sólo está formada por un término de a(n).
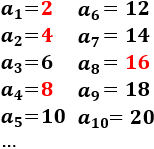 En rojo hemos indicado las potencias de 2, que son los términos de la subsucesión b(n).
Los primeros términos de b(n) son
b(1) = 2 = a(1)
b(2) = 2^2 = 4 = a(2)
b(3) = 2^3 = 8 = a(4)
b(4) = 2^4 = 16 = a(8)
b(5) = 2^5 = 32 = a(16)
...
b(n) = 2^n = a(2^(n-1))
Nota: las subsucesiones de a(n) deben estar compuestas por infinitos términos de a(n). Por ejemplo, la sucesión constante c(n) = 2 = a(1) no es una subsucesión de a(n) porque sólo está formada por un término de a(n).
En rojo hemos indicado las potencias de 2, que son los términos de la subsucesión b(n).
Los primeros términos de b(n) son
b(1) = 2 = a(1)
b(2) = 2^2 = 4 = a(2)
b(3) = 2^3 = 8 = a(4)
b(4) = 2^4 = 16 = a(8)
b(5) = 2^5 = 32 = a(16)
...
b(n) = 2^n = a(2^(n-1))
Nota: las subsucesiones de a(n) deben estar compuestas por infinitos términos de a(n). Por ejemplo, la sucesión constante c(n) = 2 = a(1) no es una subsucesión de a(n) porque sólo está formada por un término de a(n). Definición formal
Sea una sucesión y sea un subconjunto de los naturales con cardinalidad infinita. Entonces, llamamos subsucesión (o sucesión parcial) de a las sucesiones .
Propiedades
Propiedades más destacadas de las subsucesiones:
- Sea a(n) una sucesión convergente a L≠∞, entonces todas sus subsucesiones convergen a L.
- Sea a(n) una sucesión acotada, entonces todas sus subsucesiones son acotadas.
- Si una sucesión a(n) tiene dos subsucesiones que convergen a límites distintos, entonces la sucesión a(n) no converge.
- Teorema de Bolzano-Weierstrass: Sea a(n) una sucesión acotada, entonces tiene alguna subsucesión convergente.
Problema 1: Sea la sucesión alternada dada por
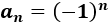 Demostrar que no converge a partir de sus subsucesiones.
Solución:
La sucesión es alternada y sus primeros términos son
Demostrar que no converge a partir de sus subsucesiones.
Solución:
La sucesión es alternada y sus primeros términos son
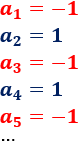 Sean las subsucesiones
Sean las subsucesiones
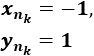 Son sucesiones convergentes porque son constantes, pero sus límites son distintos. Por tanto, a(n) no converge.
Son sucesiones convergentes porque son constantes, pero sus límites son distintos. Por tanto, a(n) no converge.
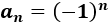 Demostrar que no converge a partir de sus subsucesiones.
Solución:
La sucesión es alternada y sus primeros términos son
Demostrar que no converge a partir de sus subsucesiones.
Solución:
La sucesión es alternada y sus primeros términos son
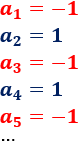 Sean las subsucesiones
Sean las subsucesiones
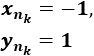 Son sucesiones convergentes porque son constantes, pero sus límites son distintos. Por tanto, a(n) no converge.
Son sucesiones convergentes porque son constantes, pero sus límites son distintos. Por tanto, a(n) no converge.Problema 2: Sea la sucesión alternada dada por
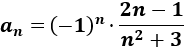 Calcular el límite de las siguientes subsucesiones de a(n):
Calcular el límite de las siguientes subsucesiones de a(n):
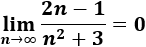 Los términos de a(n) van cambiando de signo, pero aproximándose a 0.
Como consecuencia de la convergencia de a(n), todas las subsucesiones de a(n) convergen también a 0.
Los términos de a(n) van cambiando de signo, pero aproximándose a 0.
Como consecuencia de la convergencia de a(n), todas las subsucesiones de a(n) convergen también a 0.
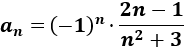 Calcular el límite de las siguientes subsucesiones de a(n):
Calcular el límite de las siguientes subsucesiones de a(n):
- x(n) = a(2n)
- y(n) = a(2n+1)
- z(n) = a(n^2)
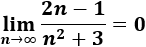 Los términos de a(n) van cambiando de signo, pero aproximándose a 0.
Como consecuencia de la convergencia de a(n), todas las subsucesiones de a(n) convergen también a 0.
Los términos de a(n) van cambiando de signo, pero aproximándose a 0.
Como consecuencia de la convergencia de a(n), todas las subsucesiones de a(n) convergen también a 0.
Más problemas: Subsucesiones: concepto, propiedades y problemas resueltos
Otros recursos de sucesiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente