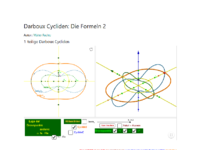
Darboux Cycliden: Die Formeln 2
Diese Aktivität ist eine Seite des geogebra-books conics bicircular-quartics Darboux-cyclides (April 2021)
verbessert 25.04.
Diese Aktivität ist auch eine Seite des geogebra-books Moebiusebene
1-teilige Darboux Cycliden besitzen in Normalform eine implizite Gleichung des Typs:
mit reellen . Die Cycliden sind symmetrisch zu den 3 Koordinatenebenen, die für die Berechnungen
wieder als komplexe Zahlenebenen betrachtet werden.
Man vergleiche dazu die Seite Darboux Cycliden: die Formeln über 2-teilige Cycliden.
Auch 1-teilige Cycliden treten immer zusammen mit einer Schar konfokaler Cycliden auf.
Die Schnitte mit den Koordinatenebenen sind 1-teilige bizirkulare Quartiken, deren Brennpunkte auf den Achsen
(*) Quadrupel des Typs bilden mit .
Die Schneitelpunkte auf den Achsen:
Aus berechnet man die Scheitelpunkte , ,
und mit die Scheitelpunkte auf der -Achse.
Die Brennpunkte:
Mit berechnet man beispielsweise: , siehe (*).
Auf jeder der 3 Achsen liegen je 2 der Brennpunkte der zugehörigen Koordinatenebenen;
insgesamt sind es wieder 3*4 Brennpunkte.
Umgekehrt berechnet man aus dem Scheitel und dem Brennpunkt die Koeffizienten , und damit
.
Konfokale Cycliden:
Sind zu einer Darboux Cyclide die Koeffizienten und damit die Brennpunkte berechnet, so erhält man durch
Vorgabe eines Scheitelpunktes, beispielsweise auf der -Achse, die Koeffizienten der konfokalen Cycliden:
Die Fokal-Kurven berechnet man, indem einer der anderen Brennpunkte auf einer Achse als Scheitelpunkt gewählt wird:
beispielsweise wähle man in der -Ebene zu den Brennpunkten (s.o) den Scheitelpunkt auf der -Achse.
Nähert sich ein Scheitelpunkt einem solchen Brennpunkt, so verflacht die zugehörige Cyclide zu einem
Flächenstück mit der zugehörigen Fokal-Kurve als Randkurve.
Die Fokal-Kurven schneiden die Achsen in Brennpunkten.
Die einzelnen Cycliden einer konfokalen Schar werden stets nur von einer der 3 Fokal-Kurven geschnitten.
Die Schnittpunkte sind die "Brennpunkte" auf den Cycliden: in diesen Punkten entstehen oder verschwinden
die Kreise auf den Cycliden! Siehe die Aktivität circles on darboux cyclides 1-sheet.Bemerkung(en):
Sofern keine Rotationssymmetrie vorliegt, existieren 3 verschiedene Fokal-Kurven, in jeder Koordinatenebene je eine.
Jede Cyclide einer solchen Schar von konfokalen Darboux Cycliden wird von einer der Fokal-Kurven in 4 Punkten geschnitten.
Diese Punkte sind die "Brennpunkte" auf der Fläche. Auf Cycliden diesen Typs existieren 2 Kreisscharen.
Die Kreise einer dieser Kreisscharen beginnen in einem der Fokal-Kurven-Schnittpunkte und
verschwinden in einem "gegenüberliegenden Brennpunkt" vergleiche circles on darboux cyclides 1-sheet.
Auf 1-teiligen Darboux Cycliden gibt es nicht mehr als 2 verschiedene Kreisscharen, und daher existieren
auf diesen Flächen keine 6-Eck-Netze aus Kreisen! | konfokale
1-teilige
Darboux Cycliden |  | erstellt mit
obigem
Applet |