Clasificación de los triángulos
Contenido
- Clasificación de los triángulos según los lados
- Clasificación de los triángulos según los ángulos
Clasificación de los triángulos
Los triángulos se clasifican en dos formas no excluyentes: por la relación de las medidas de los lados y por la medida de los ángulos interiores.
Clasificación de los triángulos según sus lados
La relación entre las medidas de los tres lados clasifica a los triángulos en:
- Triángulo Equilátero
- Triángulo Isósceles
- Triángulo Escaleno.
Triángulo Equilátero
Un triángulo es equilátero cuando los tres lados son congruentes, es decir, las medidas de sus tres lados son iguales.
Triángulo Isósceles
Un triángulo es isósceles cuando las medidas de dos de sus lados son iguales, es decir, dos lados son congruentes.
Triángulo Escaleno
Un triángulo es escaleno cuando las medidas de sus lados son diferentes entre sí, es decir, no tiene lados congruentes.
Clasificación de los triángulos según sus ángulos
La medida de los ángulos interiores clasifica a los triángulos en:
- Triángulo rectángulo
- Triángulo acutángulo
- Triángulo obtusángulo
Triángulo rectángulo
Un triángulo es triángulo rectángulo cuando uno de sus ángulos es recto, es decir, mide 90°. Los lados que forman el ángulo recto reciben el nombre de catetos mientras que el lado opuesto al ángulo recto recibe el nombre de hipotenusa. La hipotenusa es el lado de mayor longitud del triángulo.
Triángulo acutángulo
Un triángulo es acutángulo cuando los tres ángulos son agudos, es decir, cada uno mide menos de 90°
Triángulo obtusángulo
Un triángulo es obtusángulo cuando uno de sus ángulos es obtuso, es decir, mide más de 90° y menos de 180°
Análisis de las clasificaciones de triángulos
A continuación se presentan dos applets que permiten analizar las dos clasificaciones.
En el primero, se construye el triángulo dando la medida de cada uno de los tres lados. La medida de los lados determina la medida de los ángulos y por lo tanto, se obtiene la clasificación por sus ángulos.
En el segundo, se construye el triángulo dando la medida de dos de sus ángulos y la medida de uno de los lados.
Es necesario y es suficiente dar dos ángulos y un lado porque:
- La medida del tercer ángulo se deduce aplicando la propiedad de los triángulos: la suma de la medida de los tres ángulos internos de todo triángulo equivale a 180°.
- Hay infinitos triángulos que tienen la misma forma pero diferente tamaño. La forma depende exclusivamente de los ángulos.
El análisis de los dos applets permite obtener algunas conclusiones importantes.
1. Combinación de las dos clasificaciones de triángulos
- Los triángulos isósceles pueden ser
- isósceles-acutángulos
- isósceles-rectángulos
- isósceles-obtsángulos
- Los triángulos escalenos pueden ser
- escalenos-acutángulos
- escalenos-rectángulos
- escalenos-obtsángulos
- Los triángulos equiláteros siempre son acutángulos y como los tres ángulos son congruentes, recibe también el nombre de triángulo equiángulo.
2. Relaciones entre la medida de los lados y la medidas de los ángulos opuestos
- Al lado mayor de un triángulo se opone el ángulo mayor y viceversa
- Al lado menor de un triángulo se opone el ángulo menor y viceversa
- Si un triángulo tiene dos lados congruentes, entonces tiene dos ángulos congruentes. Este triángulo es el isósceles.
3. Desigualdad triangular
En todo triángulo, la suma de las medidas de dos lados es mayor que la medida del tercer lado.
La desigualdad triangular se analiza en el applet siguiente, en el cual se dan las medidas de los tres lados a, b y c.
El procedimiento para dibujar un triángulo dados los 3 lados es:
- Se toma uno de los lados, por ejemplo, lado a, cuyos extremos son B y C
- Por el extremo C se dibuja una circunferencia con radio igual al lado b
- Por el extremo B se dibuja una circunferencia con radio igual al lado c
- Las dos circunferencias se intersecan en el punto A que corresponde al tercer vértice del triángulo.
Cuando se modifican las medidas de uno o varios lados, las dos circunferencias toman diferentes posiciones relativas como se ilustra en la figura.
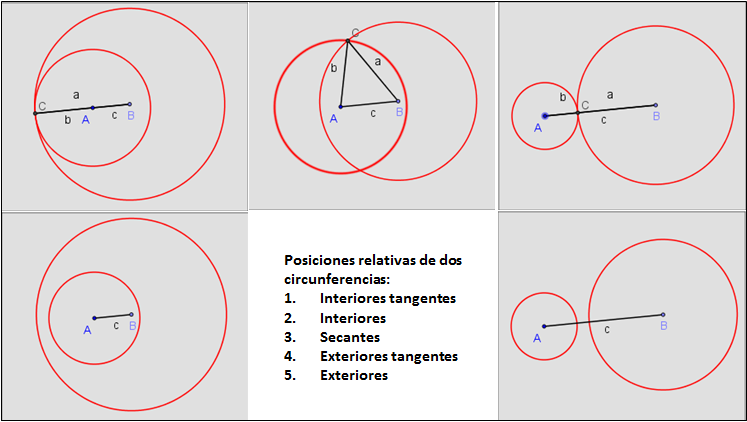
El tercer vértice del triangulo se obtiene únicamente cuando las dos circunferencias son secantes. En los demás casos, no se forma un triángulo.
Esto se comprueba con la tabla de desigualdades:
Para una terna de medidas se puede presentar uno de dos casos:
- Si las tres desigualdades son verdaderas (true), sí se forma un triángulo. Las dos circunferencias son secantes.
- Si una cualquiera de las desigualdades es falsa (false), no se forma triángulo. Las dos circunferencias no son secantes.