Folding a corner of a square sheet (inspired by “INTRASQUARES” AND “EXTRASQUARES” from Haga's book Origamics)
- Autore:
- Giovanna Valori
- Argomento:
- Geometria, Poligoni, Trasformazioni geometriche
Using paper and GeoGebra
Materials: some square sheets of paper, a ruler, a black marker pen
Task 1
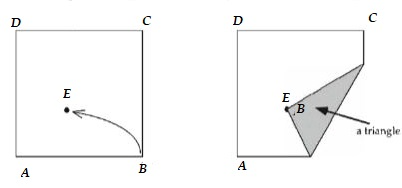
Take a square sheet of paper and label it as in the picture below. Pick a random point E on the paper and fold B to that point. How many sides does the flap of paper you get (kind of polygon) have? This depends on the position of E? Try several times with identical sheets. Formulate conjectures and try to justify them!
with GeoGebra
Answer Task 1
Task 2
What if we allow point E to be outside the square as well? Formulate conjectures and try to justify them!
Answer Task 2
Bibliography
Haga, K. (2008). Origamics. Mathematical Explorations through Paper Folding. World Scientific.
Hull, T. C. (2013). Project Origami: Activities for Exploring Mathematics (2nd ed.). A K Peters/CRC Press.