Der Einheitskreis und die Winkelfunktionen
1. Der Einheitskreis
Existiert bzw. welchen Wert hat der Sinus von 273?
Um diese Frage beantworten zu können, benutzen wir den Einheitskreis:
Darunter versteht man einen Kreis mit Radius r = 1 Einheit und Mittelpunkt M( 0| 0) im Koordinatenursprung.
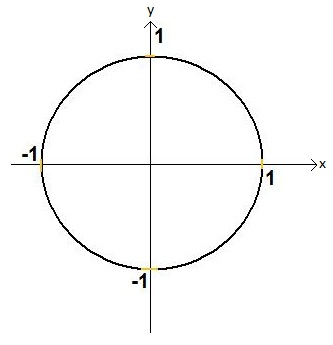
Lässt man nun einen Punkt P auf dem Einheitskreis entlanglaufen, so entstehen rechtwinklige Dreiecke. Wobei der rechte Winkel immer an der x-Achse liegt und die Hypotenuse immer aus dem Radius des Einheitskreises gebildet wird. Ihre Länge ist also immer 1.
Untersuche die Behauptung, indem du P mit der Maus verschiebst.
2. Konstruktion der Winkelfunktionen am Einheitskreis
Den Winkel, den der Radius mit der x-Achse (gegen den Uhrzeigersinn gemessen) einschließt, nennen wir . Die blaue Strecke ist also die Gegenkathete von und die rote Strecke ist die Ankathete von . Die Hypotenuse ist ja der Radius selbst, also die schwarze Strecke.
Nun gilt:
von P
von P
Auf diese Weise lassen sich Werte für und definieren, auch wenn größer ist als 90°. Diese können nun auch negativ annehmen.
Packe den Punkt P mit der Maus und lies die jeweiligen Werte für sind bzw. cos ab.
Konstruktion des Tangens am Einheitskreis
Nun ist ein Dreieck gesucht, dessen Ankathete gleich 1 ist, damit wir den Wert des tan() direkt ablesen können.