GeoGebra

An Extended Interpretation of the Concept of point estimators of location (geometric medians and geometric centers) in bounded closed domains for a discrete set of points from ℝ³

Author:Roman Chijner
There is a system of n points in a certain region. For the "average overall" characteristic of such a system, point estimates are usually used: the geometric median and the geometric center (or center of mass, the centroid of a finite set of n points). In the first case, it is a point that minimizes the function of the sum of the distances between itself and each point in the set (for three points - Fermat point), and the sum of the squares of this distances -in the second case. I propose a more extended interpretation of the concept of point estimates of the location (geometric medians and geometric centers) of a discrete set of n points not in the entire domain e.g. ℝ³, but in some domain. That is, you need to find points in this domain that extremize the sum of the distances function from them to n points of the set. 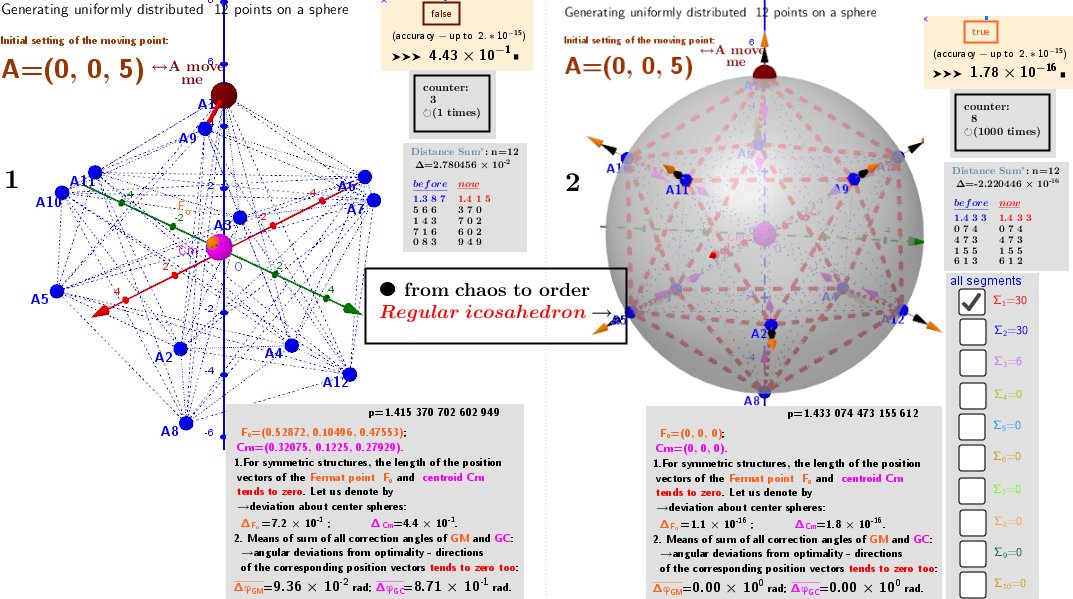In applets, a limited number of particles from ℝ³ are considered, and a circle and a sphere are considered as such a domain, i.e. point estimates are sought on a circle / sphere. The search for point estimates on a circle allows you to understand their meaning more clearly . Thus, the search for point estimates is reduced to finding the critical points of the distance sum function f (x, y, z) subject to a constraining equation g(x,y)=x²+y -R² in the case of estimation on a circle or g(x,y,z)=x²+y²+z²-R²-in the case of estimation on the sphere. The problem is solved using Lagrange multipliers. There is a system of equations: ∇f(x,y,z)= λ∇g(x,y,z). A local optimum occurs when ∇f(x,y,z) and ∇g(x,y,z) are parallel, and so ∇f is some multiple of ∇g. Algorithms are proposed for finding points corresponding to extremes: minima, maxima, and, in the case of the sphere, also saddle points of the sum of distances function.
Key points in images. Examples of point estimators of location (geometric medians and geometric centers) in bounded closed domains for a discrete set of points from ℝ³
1. Point estimators (geometric median and geometric center) defined for a discrete set of points from ℝ³

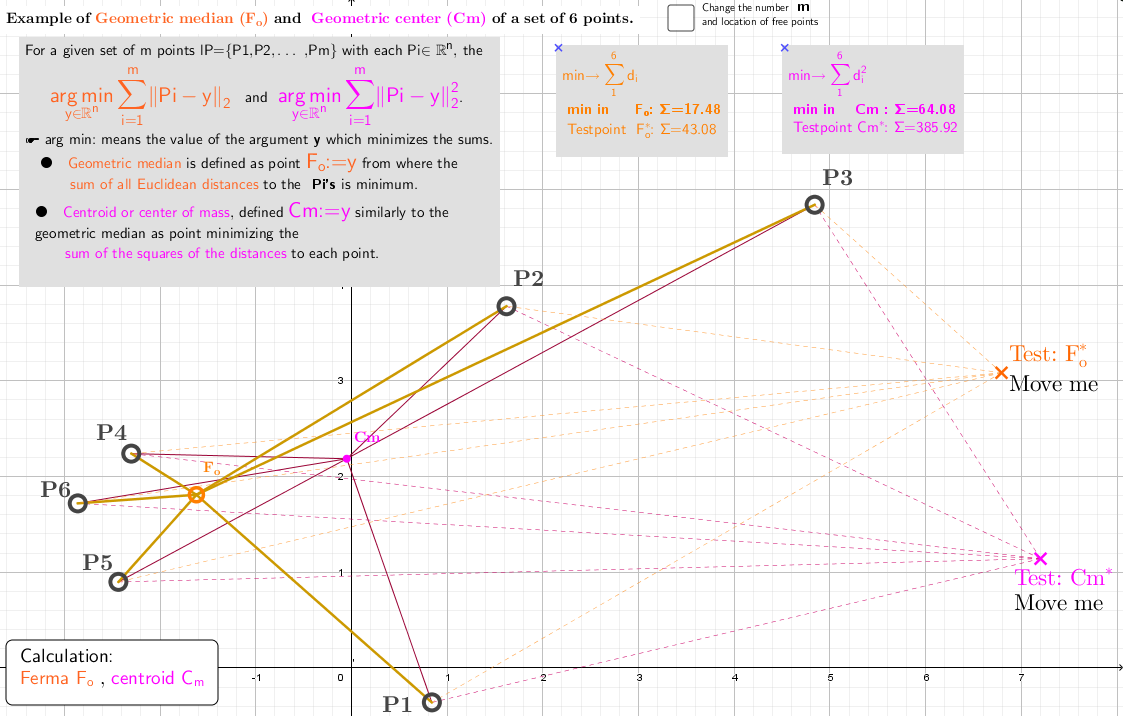
The geometric median of a discrete set of sample points in a Euclidean space is the Point minimizing the sum of distances(di) to the sample points. For triangles, this point is called the Fermat point. The geometric center  of a discrete set of sample points in a Euclidean space is the Point minimizing the sum of the squares of the distances(di2) to the sample points, can be found by a simple formula — its coordinates are the averages of the coordinates of the points.  It is also known as the centroid, center of mass of a finite set of points.

Example 1.1

Example 1.1
Example 1.1: Point estimators of location (Geometric median and Geometric center) of a discrete set of 6 points from ℝ³. Here, arg min means the value of the argument y which minimizes the sum of distances to the sample points. In this case, it is the point- Fo:=y. For the sum of the squares of the distances to the sample points, such point is Cm:=y.
2. Point estimators of location (geometric medians and geometric centers) defined in bounded closed domain: on a circle for a discrete set of points from ℝ³

Example 2.1a

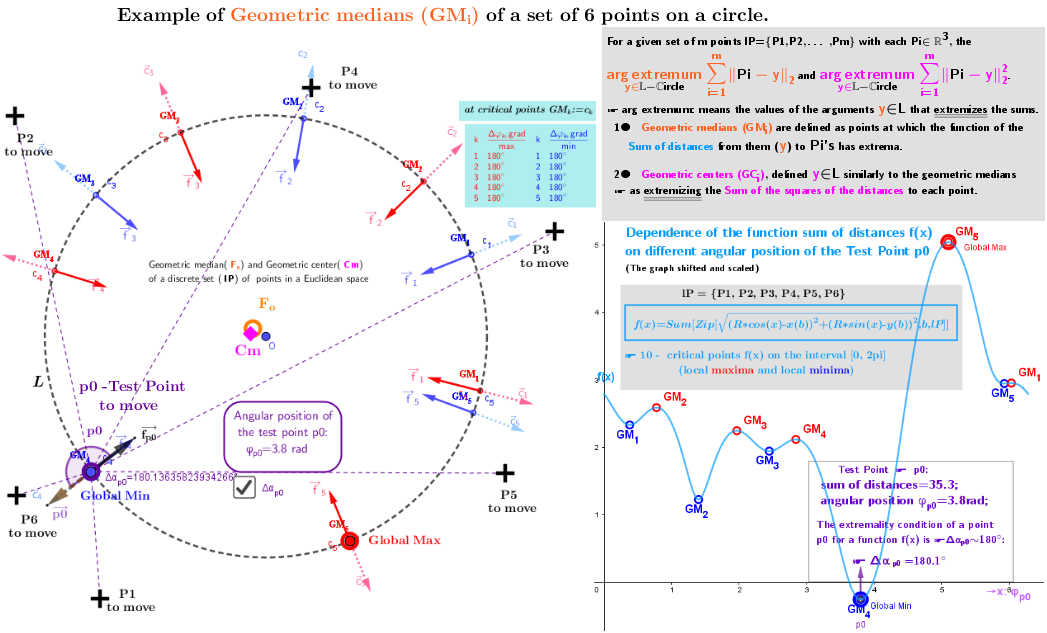
Example 2.1a
Example 2.1a: Point estimators of location (geometric medians GMᵢ) defined on a circle for a discrete set of 6 points from ℝ³

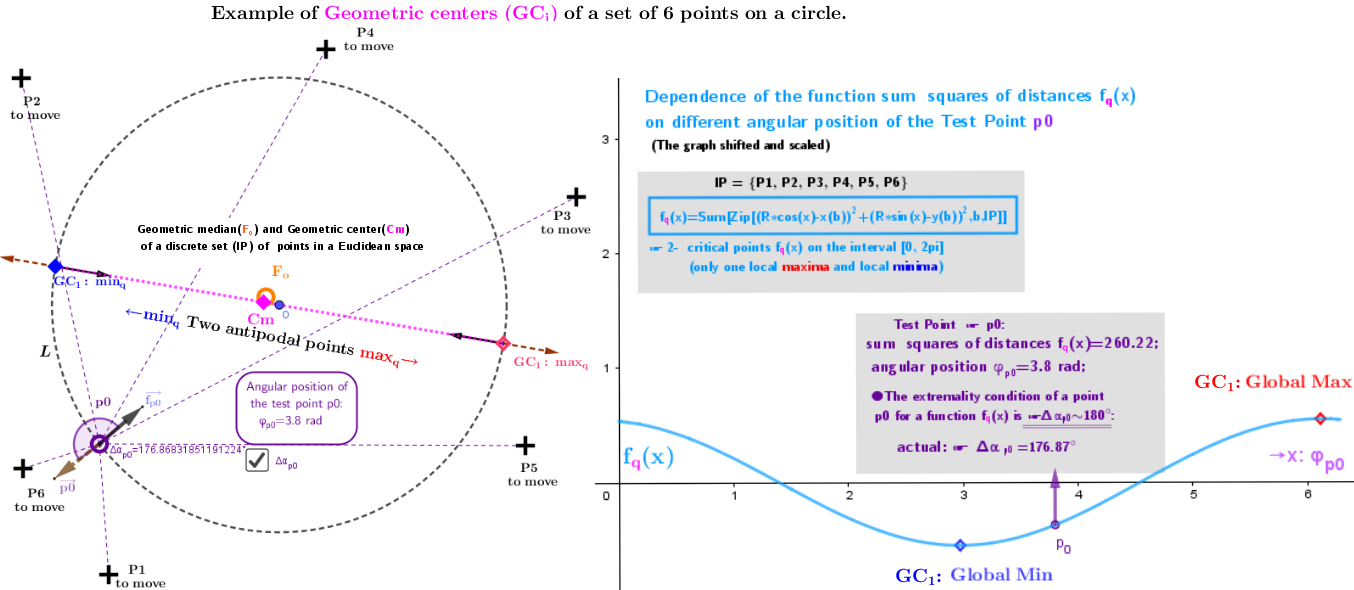
Example 2.1b

Example 2.1b
Example 2.1b: Point estimators of location (geometric centers GCᵢ) defined on a circle for a discrete set of 6 points from ℝ³

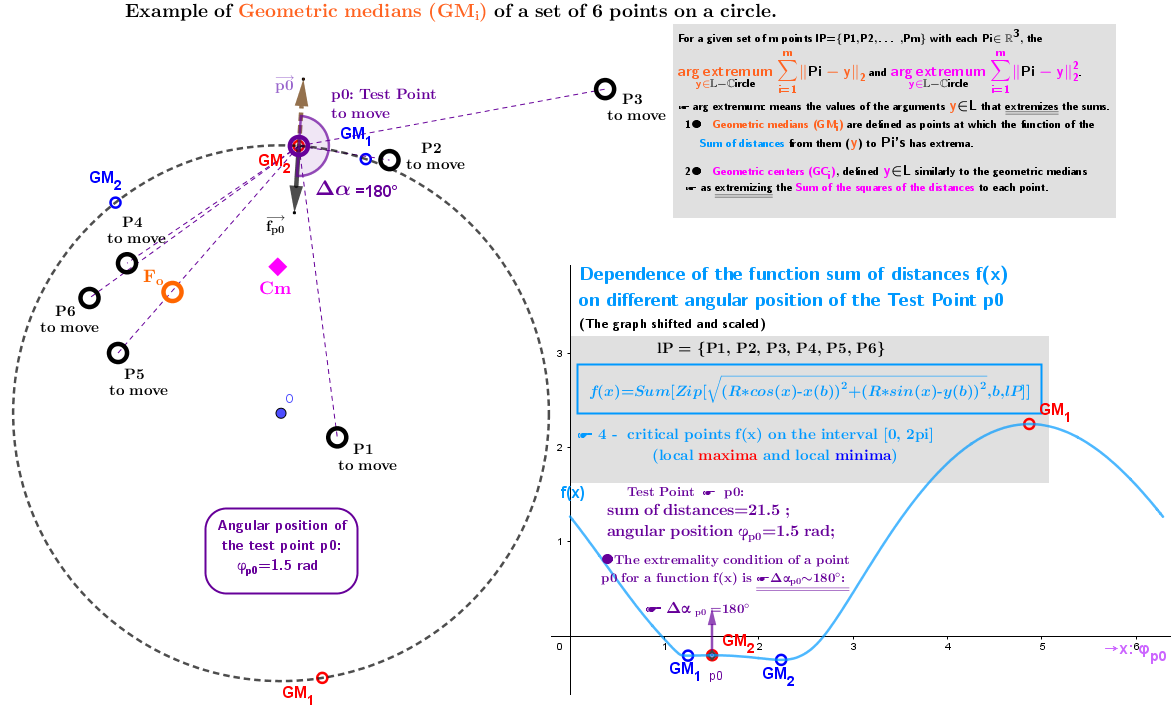
Example 2.2a

Example 2.2a
Example 2.2a: Point estimators of location (geometric medians GMᵢ) defined on a circle for a discrete set of 6 points from ℝ³

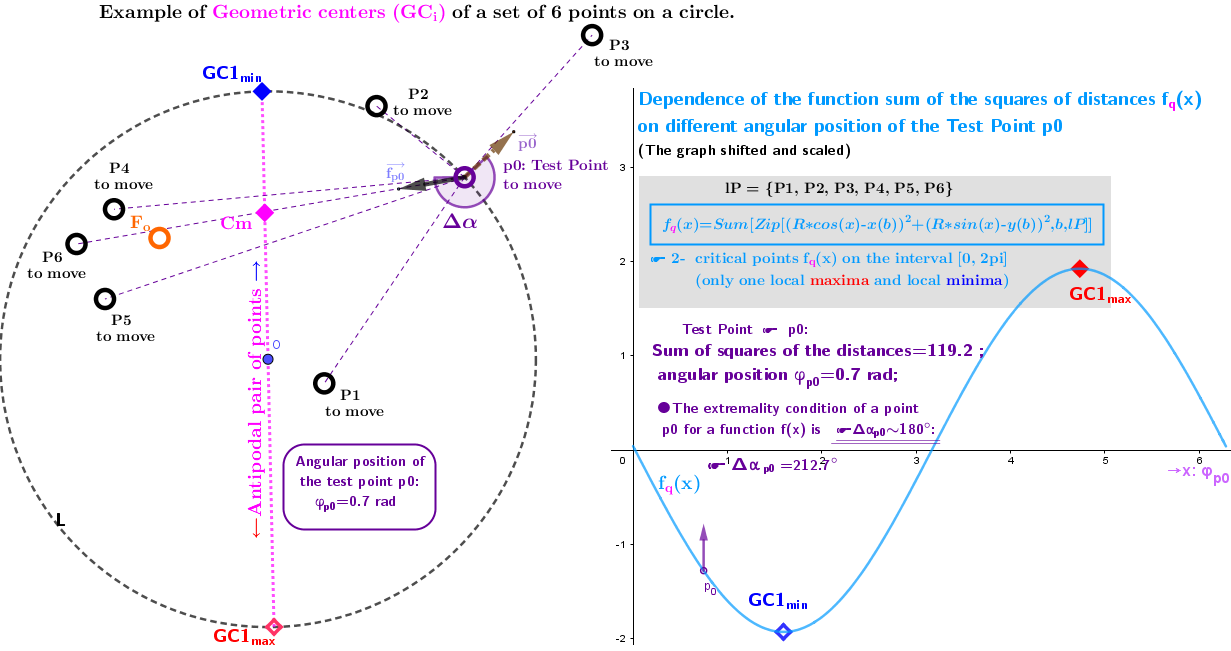
Example 2.2b

Example 2.2b
Example 2.2b: Point estimators of location (geometric centers GCᵢ) defined on a circle for a discrete set of 6 points from ℝ³

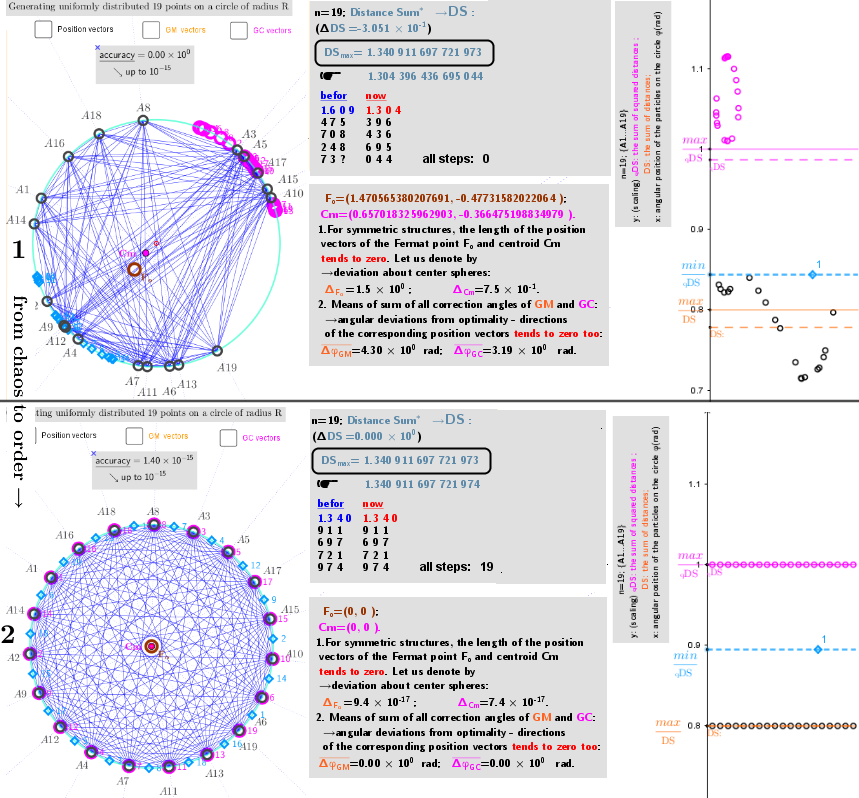
Example 2.3

Example 2.3
Example 2.3 Generating a uniform distribution of points on a circle. Let L be a circle of radius R around the point O: L:={x∈ℝ2: ||x||=R}. There is a set lP={A1, A2,...,An} of n movable free points on a circle. Problem: use the method of Lagrange multipliers find such their distribution corresponding to the maximum sum of all their mutual distances. This means need to find out such mutual arrangement of "repulsive" set of particles on a circle, when each point of this set is Geometric median (GM) of the remaining n-1 points. We assume that the equilibrium - stationary state in system of "charges" is reached if the sum of their mutual distances is maximal. Iterative approach of particle placement is applied for achieving a stationary state.
3. Point estimators of location (geometric medians and geometric centers) defined in bounded closed domain: on a sphere for a discrete set of points from ℝ³

Example 3.1

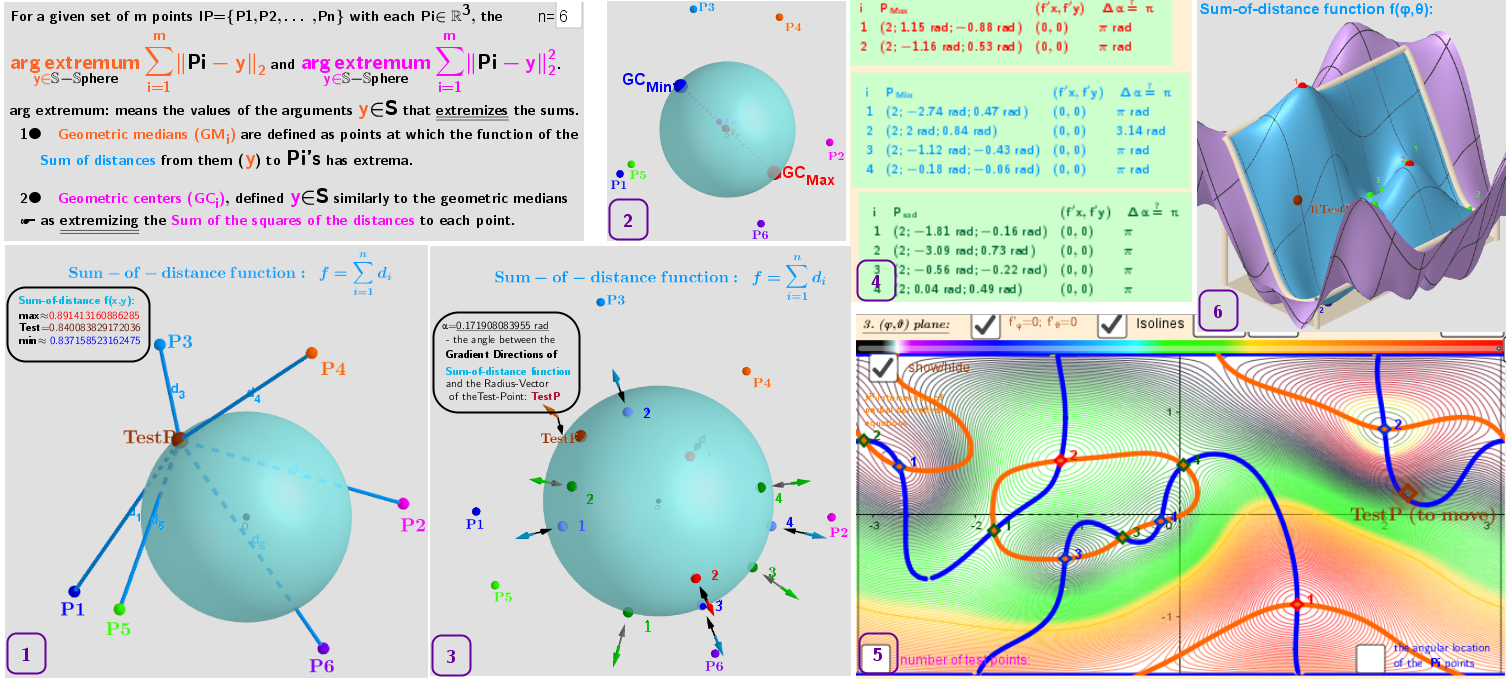
Example 3.1
Example 3.1: Point estimators of location (geometric medians GMᵢ and geometric centers GCᵢ) defined on a sphere for a discrete set of 6 points from ℝ³ 1. 6 Points in ℝ³ and the search their Point Estimators: geometric medians and geometric centers on the surface of the sphere. 2. Regardless of the number of points they have only two geometric centers on the surface of the sphere: two antipodal points. 3. The existing distribution of 6 points in this example give ten geometric medians on the surface of the sphere: 2 maxima, 4 minima and 4 saddle critical points for the sum-distance function. The vectors ∇f and ∇g are parallel at these points. 4. Table of coordinates of the critical points of distance sum-distance function f(φ,θ) over a rectangular region on the surface of the sphere: φ∈[-π,π](x-Axis), θ∈[-0.5π,0.5π](y-Axis). They are found using Lagrange multipliers as finding the Extreme values of the function f(x,y,z) subject to a g(x,y,z)=0 (constraining equation: g(x,y,z)=x²+y²+z²-R²). The table also contains partial derivatives and Angles between the vectors ∇f and ∇g at these critical points. 5. (φ;θ) -plane of the angular coordinates of points on the sphere: φ∈[-π,π], θ∈[-0.5π,0.5π]. The colored Isolines are qualitatively indicate the type of critical points. The intersection of implicit functions of the equations of zero partial derivatives: f'φ(φ, θ)=0; f'θ(φ,θ)=0 over a rectangular region φ∈[-π,π], θ∈[-0.5π,0.5π] -are solutions (critical points) of the Lagrange equations. 6. Graphic of the distance sum function f(φ, θ) over a rectangular region φ∈[-π,π], θ∈[-0.5π,0.5π] with the positions of the corresponding maxima/minima and saddles -its critical points.

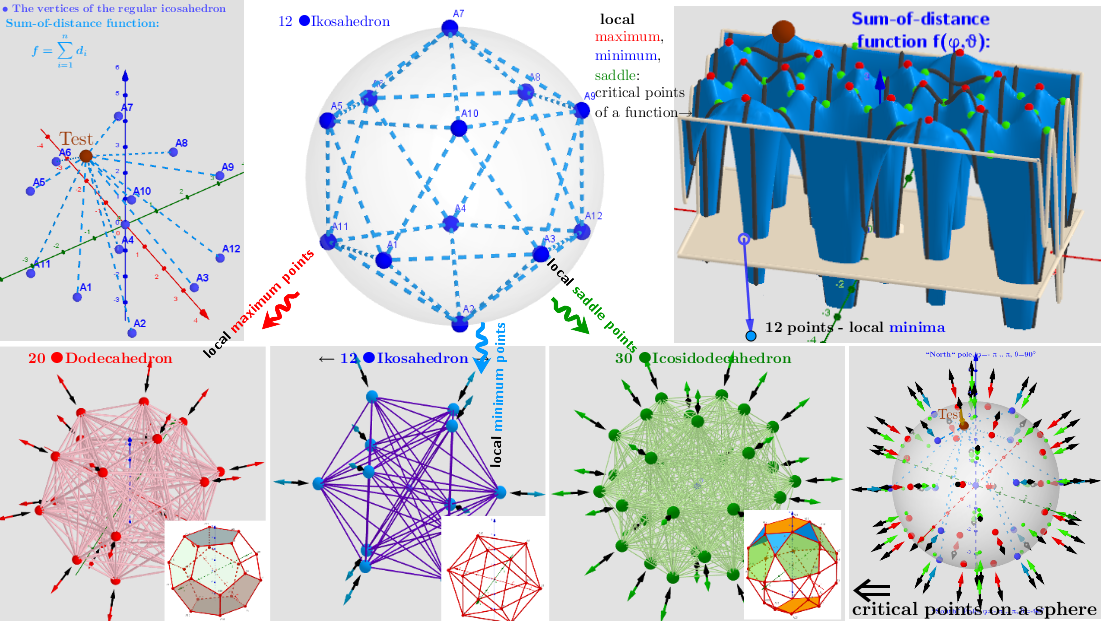
Example 3.2

Example 3.2
Example 3.2: The uniformly distribution of Point estimators of location -geometric medians on a sphere, „induces“ by the discrete sample of uniformly distribution points in the 3-D space. Description is in https://www.geogebra.org/m/y8dnkeuu. Here, the 12 vertices of the Icosahedron "induce" the vertices of the other three polyhedra: 20 ●Dodecahedron← 12 ●Icosahedron →30 ●Icosidodecahedron.

Example 3.3

Example 3.3
Example 3.3 Generating a uniform distribution of points on a sphere. Let S be a sphere of radius R around the point O: S:={x∈ℝ³: ||x||=R}. There is a set lP={A1, A2,...,An} of n movable free points on a sphere. Problem: use the method of Lagrange multipliers find such their distribution corresponding to the maximum sum of all their mutual distances. This means need to find out such mutual arrangement of "repulsive" set of particles on a sphere, when each point of this set is Geometric median (GM) of the remaining n-1 points. We assume that the equilibrium - stationary state in system of "charges" is reached if the sum of their mutual distances is maximal. Iterative approach of particle placement is applied for achieving a stationary state.

New Resources

Discover Resources

Discover Topics