Producto cruz o vectorial
Definicion.
El producto cruz, también llamado producto vectorial, es un tipo de producto que se lleva a cabo entre dos vectores y da como resultado otro vector, perpendicular al plano definido por los dos primeros.
El producto cruz entre dos vectores cualesquiera a y b, da como resultado otro vector R, matemáticamente se escribe de la siguiente forma:
a × b = R
Se lee así: “a cruz b igual a R”.
En texto impreso, los vectores se escriben con letra negrita, o con una flecha encima de la letra, para distinguirlos de su magnitud o módulo. Para este se emplean, indistintamente, las barras de módulo y las letras corrientes, así se tiene que el valor absoluto del vector a simbólicamente se escribe así:
│a│= a
El valor absoluto o módulo del producto vectorial entre dos vectores se calcula multiplicando el módulo de ambos vectores por el seno del ángulo θ que hay entre ellos:
R = a∙b∙sen θ
La dirección del vector R es perpendicular a la de los vectores a y b. El sentido de R es dextrógiro de a hacia b y en la práctica se determina usando la regla de la mano derecha, que consiste en posicionar los dedos índice, medio y pulgar de la mano derecha así:
- Se coloca el dedo índice siguiendo al vector a
- Con el dedo medio se sigue al vector b
- El dedo pulgar, extendido, señala la dirección y el sentido del vector R.
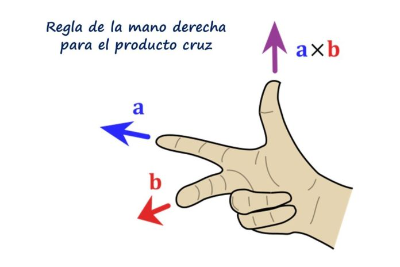
Se aconseja al lector colocar su mano derecha tal como muestra la figura, el índice apuntando a la izquierda representa al vector a, el dedo medio sigue a b y apunta directamente hacia el lector, finalmente, el pulgar señala hacia arriba, señalando dirección y sentido del vector a × b = R.
Propiedades del producto cruz.
-El producto cruz o vectorial entre dos vectores siempre resulta en otro vector.
-Un producto cruz no es conmutativo, por lo tanto: a × b ≠ b × a.
-Para el producto cruz se cumple que: a × b = − (b × a). A esta propiedad se la llama anti-conmutatividad.
-El vector resultante del producto vectorial entre dos vectores es perpendicular (normal) a dichos vectores.
-De lo anterior se deduce que el producto vectorial entre vectores con la misma dirección es nulo. En particular a × a = 0.
-El producto cruz cumple la ley distrbutiva respecto a la suma: a × (b+c) = a × b + a × c
-Si m es un escalar, entonces m (a × b) = m a × b = a × m b
Ejemplo
Suponiendo que los vectores a y b son:
- a = 5 i − j + 4 k
- b = −i + 0j +7 k
