Méthode des réctancle
Pour une meilleur approximation de l'aire qu'on cherche on pourra poursuit comme suit:
diviser l’intervalle en n = 2 morceaux, puis de construire les rectangles associés
comme cela :

l’aire Somme 2 est plus grande que l’aire sous la courbe car tous les rectangles
correspondants sont au-dessus de la courbe.
De même, l’aire Somme 2 est plus petite que l’aire sous la courbe car tous les rectangles verts
correspondants sont en-dessous de la courbe.
En réalité Somme 1 et Somme 2 permettent d’avoir un encadrement de la véritable aire sous la courbe :

On peut améliorer cette première approximation par : diviser l’intervalle en n =4 morceaux
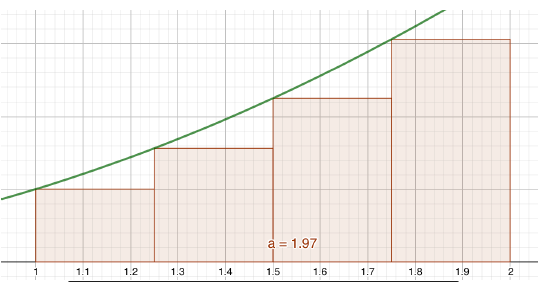
Pour une bonne aproximation on peut tout simplement augmenter le nombre de rectangles
Cette méthode des rectangles consiste en fait à partager un intervalle en n morceaux et à construire
n rectangles comme on a vu précédemment. Enfin, on réalisait la somme des aires de ces rectangles.
L'aire
Pour que l'aire tende vers la valeur exacte de l’aire sous la courbe, il faut que n tende vers l’infini. on note
qand quand
Alors la somme qui était jusqu’à présent discrète devient continue. Dès lors les notations changent et on écrit AIRE de la courbe délimité par et
Il s’agit de la même somme que précédemment, la seule chose qui change c’est que cette dernière
est continue.
