Primjena linearne ovisnosti u praktičnim zadatcima
Zadatak 1
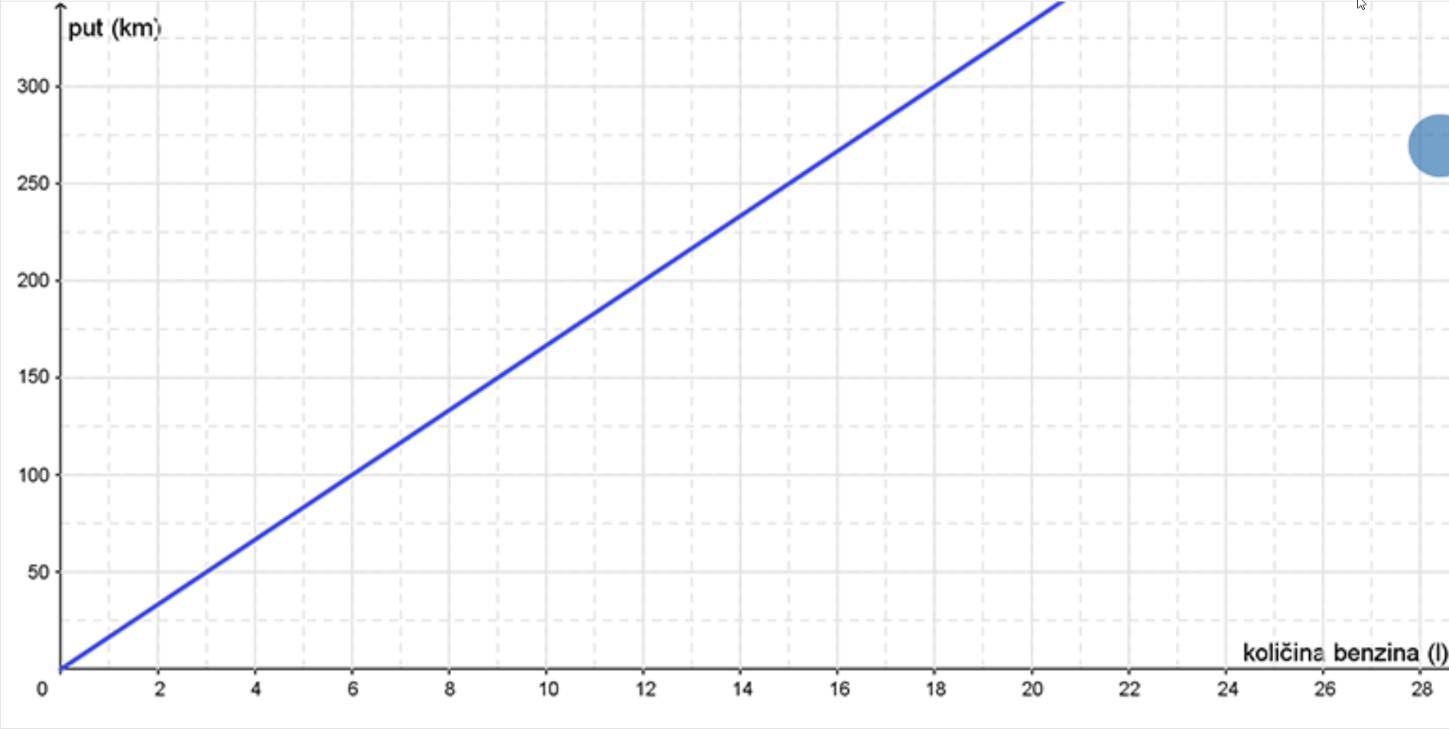
a)
Koliku udaljenost će prijeći automobil sa 9 L benzina?
b)
Koliko će benzina potrošiti automobil da prijeđe 300 km?
c)
Koliko će benzina potrošiti automobil da prijeđe 100 km?
d)
Koliku udaljenost će prijeći automobil sa 15 L benzina?
Zadatak 2
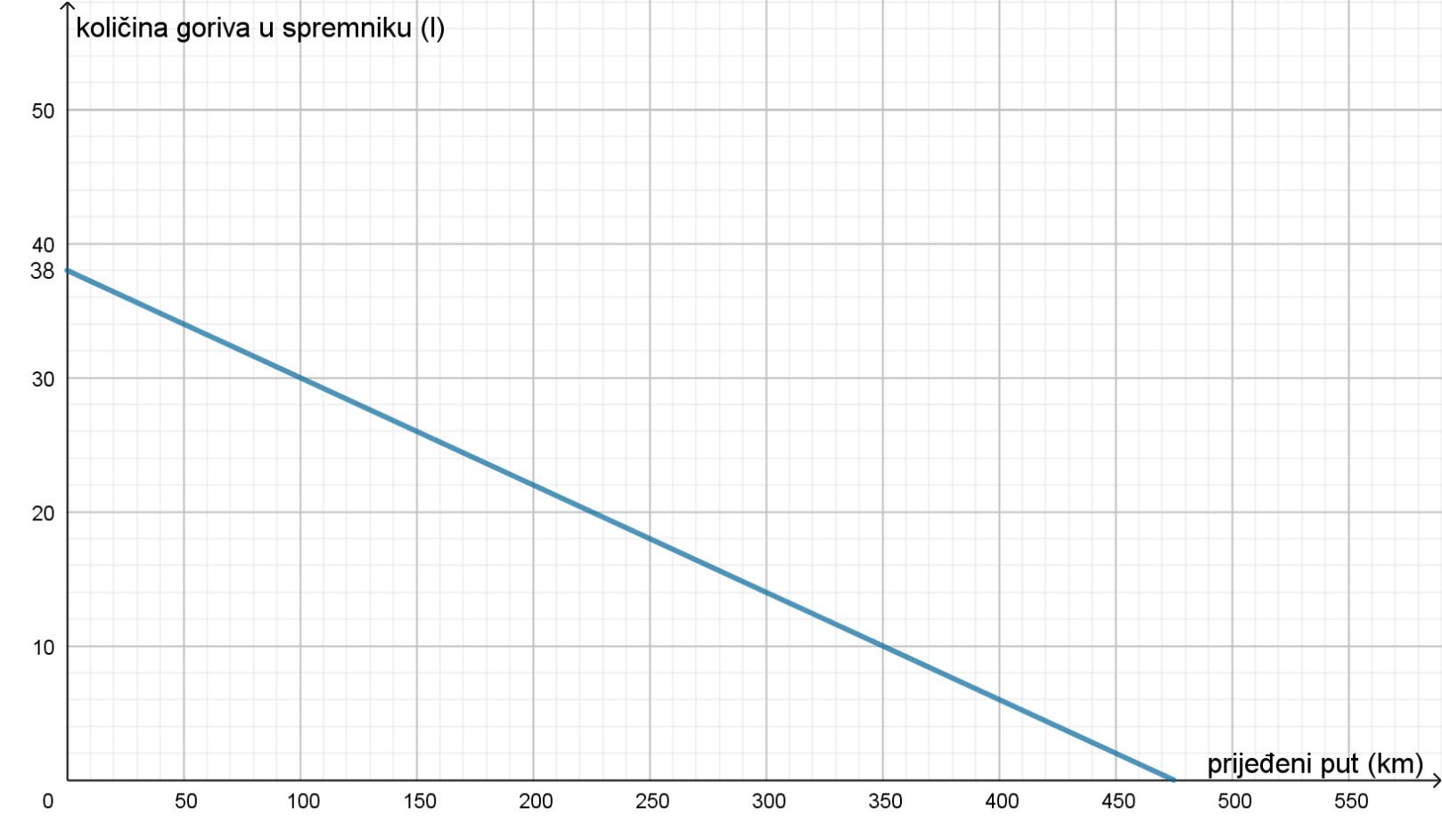
a)
Kolika je količina goriva bila u spremniku na početku puta?
b)
Kolika je prosječna potrošnja goriva (u litrama na 1 km)?
c)
Kako glasi formula linearne ovisnosti koja opisuje količinu preostalog goriva u spremniku automobila u ovisnosti o prijeđenom putu?
Zadatak 3
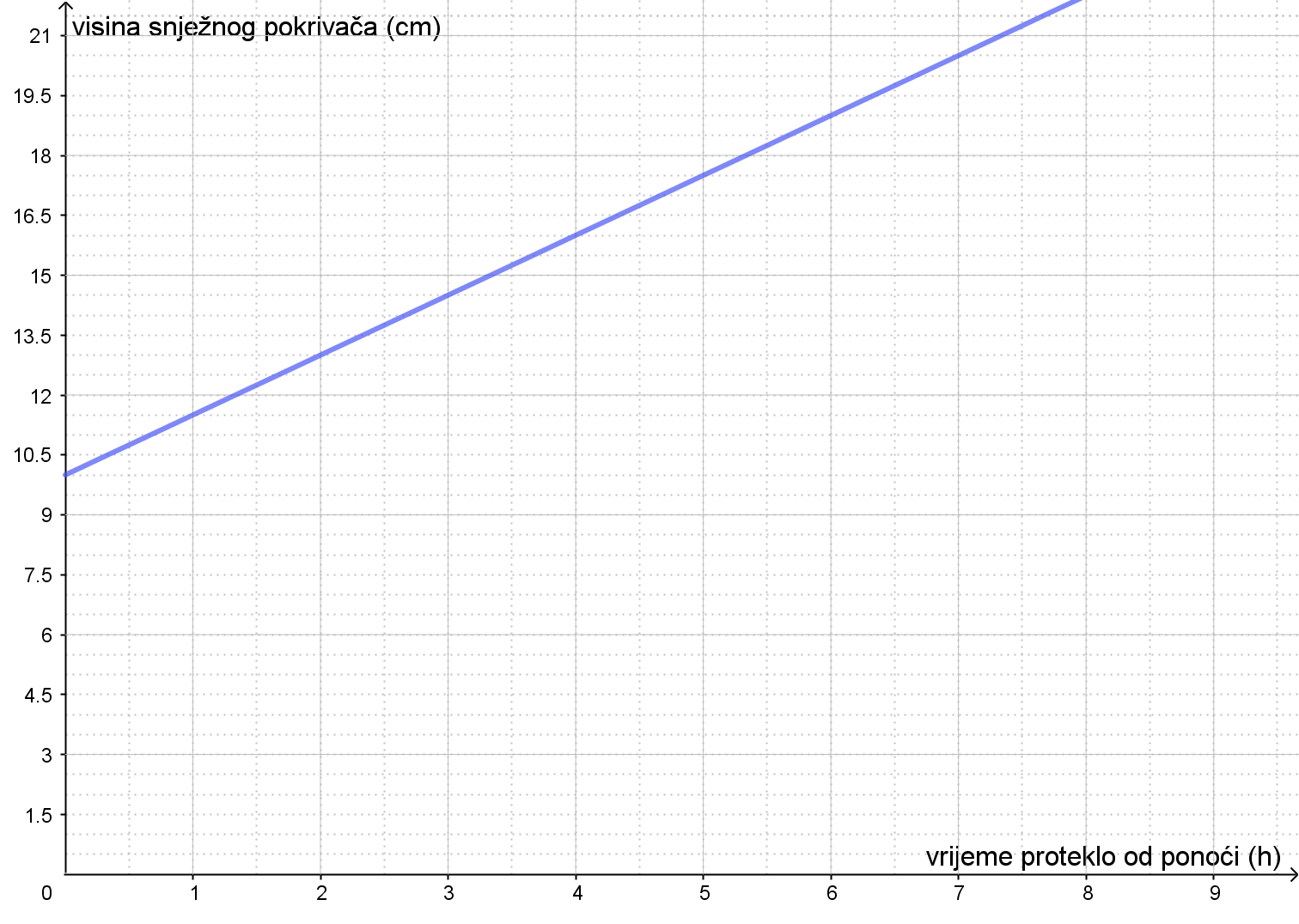
a)
Kolika je bila visina snijega u ponoć kad je započeto mjerenje?
b)
Kolika je bila visina snježnog pokrivača u 4 sata ujutro?
c)
U koliko sati je visina snijega bila 19 cm?
d)
Zapiši formulom linearnu ovisnost koja opisuje visinu snježnog pokrivača u ovisnosti o proteklom vremenu.
Zadatak 4
a)
Kako glasi formula linearne ovisnosti visine mjesečnog računa o broju odvoza? (koristi uobičajene oznake za zapis zavisne i nezavisne veličine, tj. y i x)
b)
Koliki je račun za odvoz smeća ako je ono odvezeno 3 puta u mjesec dana?
c)
Koliko je puta u mjesecu odvezeno smeće ako je iznos računa 40 kn?
Zadatak 5
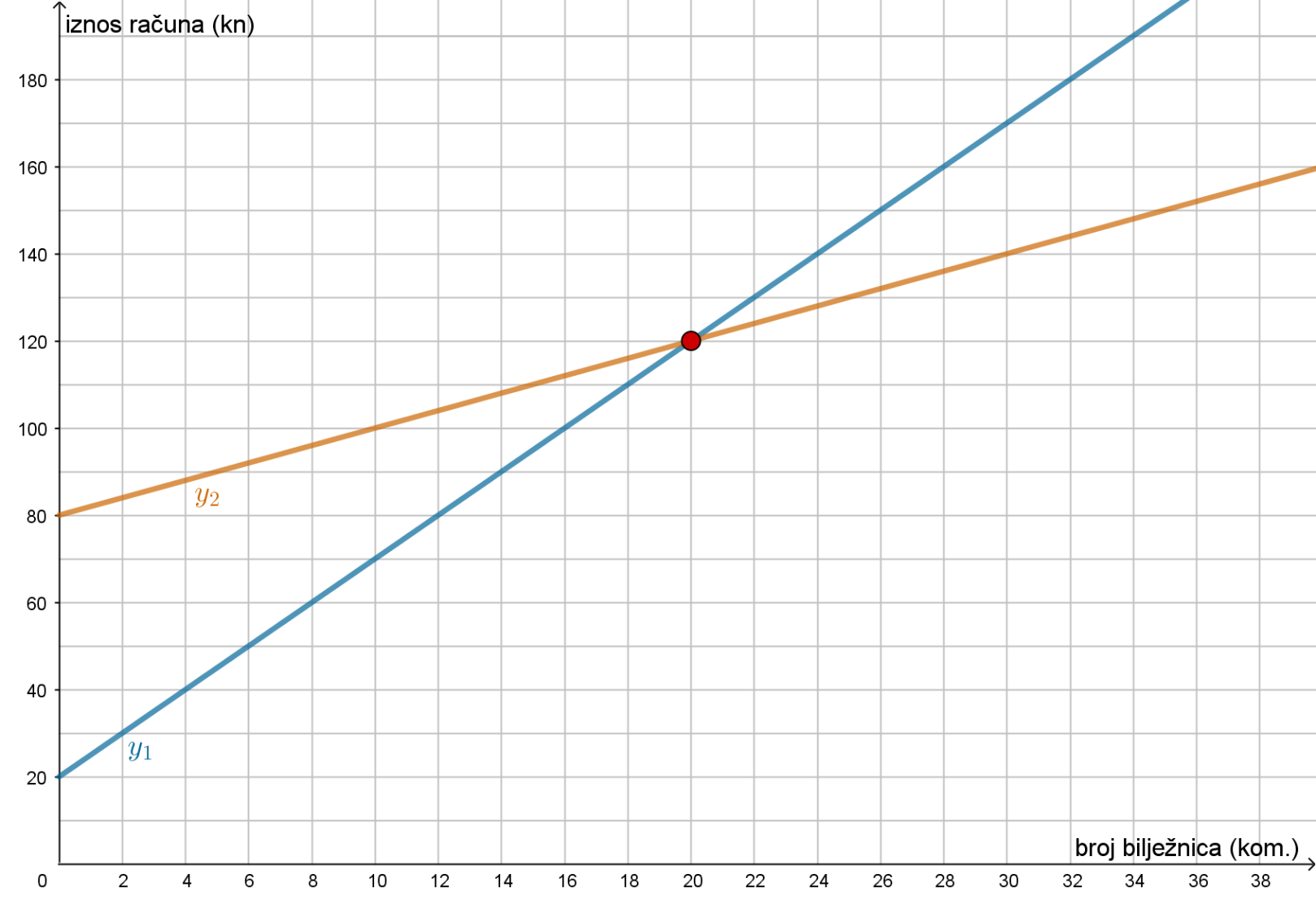
a)
Koliko tvrtke naplaćuju fiksni iznos za dizajn slogana?
b)
Napiši formulom linearnu ovisnost koja prikazuje ovisnost iznosa računa o broju kupljenih bilježnica, za obje tvrtke.
c)
Koliko bi učenici trebali naručiti bilježnica da bi trošak u obje tvrtke bio jednak?
d)
Koja je tvrtka povoljnija ako učenici žele naručiti 18 bilježnica?
e)
Koja je tvrtka povoljnija ako učenici žele naručiti 26 bilježnica?
f)
Koliko je iznosio račun za bilježnice, ako su učenici kupili 30 bilježnica po povoljnijoj cijeni?
Zadatak 6
a)
Napiši formulu kojom se može izračunati iznos novca koji je Dajana prikupila tijekom mjeseca, ovisno o tome koliko je sati toga mjeseca čuvala Petra. (koristi uobičajene oznake za zapis zavisne i nezavisne veličine, tj. y i x)
b)
Koliko je novca sakupila Dajana prethodnog mjeseca, ako je čuvala Petra ukupno 30 sati?
c)
Koliko sati mora Dajana čuvati Petra ovoga mjeseca, ako želi sakupiti 380 kn?
d)
Cijena novog računala koje Dajana želi kupiti je 4500 kn. Koliko bi prosječno sati svakoga mjeseca trebala Dajana čuvati Petra, ako želi sakupiti taj novac za 10 mjeseci? (dobiveni rezultat zaokruži na cijelo)
Zadatak 7
a)
Zapiši formulu za izračun temperature zraka u hladnjaku ovisno o proteklom vremenu (u minutama) od uključenja hladnjaka. (koristi uobičajene oznake za zapis zavisne i nezavisne veličine, tj. y i x)
b)
Kolika je bila temperatura u hladnjaku nakon 17 minuta?
c)
Nakon koliko će vremena temperatura u hladnjaku biti 14°C?
d)
Koliko treba vremena da hladnjak postigne optimalnu temperaturu? (zaokruži na cijelo)