Grundsituation 3D → 2D
Aus der dreidimensionalen Z-förmigen Figur, die durch Falten längs a und f entstanden ist, wird wieder eine ebene Figur erzeugt, indem die Rechtecke F und EZ in die xy-Ebene zurück gefaltet werden.
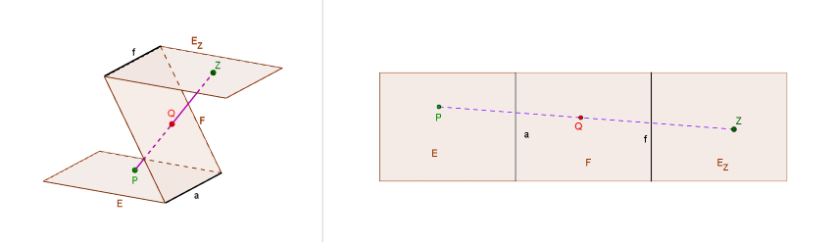
Wir konzentrieren uns hier zunächst auf die Abbildung eines beliebigen Punktes P.
Wenn ZP die Ebene F in der 3D-Darstellung in Q schneidet, so wird aus der Strecke ZP in der ebenen Darstellung die direkte Verbindung von Z und P, hier gestrichelt gezeichnet.
Anschaulich gesagt müsste die Strecke ZP elastisch sein und wird beim Rückfalten in die Länge gezogen.
Der Schnittpunkt Q muss dann irgendwo in dem mittleren Bereich F auf dieser Verbindungslinie ZP liegen.
Damit ist er aber noch nicht eindeutig festgelegt, wir bräuchten in der Ebene noch eine zweite Linie.
Wie man dies erreicht, wird im Folgenden erarbeitet.
Auf diese Weise kann dann die räumliche Konstruktion durch eine ebene Konstruktion ersetzt werden.
Seit dem Aufkommen von 3D-DGS ist dies eigentlich nicht mehr erforderlich, sondern mehr historisch interessant. Zu Zeiten, wo mit Zirkel und Lineal konstruiert werden musste bis zur 2D-DGS war diese eine wesentliche Reduktion der Komplexität.
Bindet man schließlich P an eine Parabel, erzeugt die Ortslinie von Q und verändert die Parabel mittels Brennpunkt und Leitlinie, sieht man auch, wie sich die Ortslinie von Q verändert, was in der zweiten Aufgabenserie noch in zwei Fallunterscheidungen betrachtet wurde.
Siehe Lietzmann (1949): Elementare Kegelschnittlehre S. 128