Bisectriz como lugar geométrico
Criterios de semejanza de triángulos
Construcción de la bisectriz con regla y compás
Demostración matemática (geométrica)
Los tres problemas clásicos de la antigüedad
Los problemas con regla y compás sólo permiten usar para resolverlos un lápiz, una regla no graduada y un compás. Los tres problemas clásicos de la antigüedad son la trisección del ángulo, la cuadratura del círculo y la duplicación del cubo. Todos ellos han sido resueltos: se ha probado que todos son imposibles de construir. 1. La trisección del ángulo: dividir en tres partes iguales un ángulo cualquiera usando únicamente un compás y una regla no calibrada. La construcción general para la trisección, el deseo de generalización para la división de un ángulo en un número cualquiera de partes iguales y un problema asociado a la división de ángulos como es la construcción de polígonos regulares con cualquier número de lados hicieron que muchos matemáticos helenos abordaran el problema: Hipócrates de Quío e Hipias de Elis en el siglo V a.C.; Nicomedes, Arquímedes y Apolonio de Perga en el siglo III a.C. Los tres últimos encontraron soluciones mecánicas, es decir, soluciones apoyadas en curvas mecánicas (como la espiral de Arquímedes -que tiene muchas aplicaciones actualmente-), que no se generan con regla y compás. En 1837 Fierre L. Wantzel demostró, usando la teoría de grupos (de Galois), que un ángulo se puede trisecar con regla y compás si, y sólo si, el polinomio es reducible, cosa que no ocurre para cualquier valor de (si es recto o llano, sí). Este problema quedó zanjado con este resultado. Por su parte, Gauss demostró que un polígono regular de n lados (n3) es constructible con regla y compás si, y sólo si, o bien n es una potencia de 2, o bien los primos impares presentes en la descomposición de n son potencias unitarias de números de Fermat, esto es, de la forma = para algún valor entero no negativo de m (no valen potencias mayores que 1 de números de Fermat; por ejemplo, 9=, por lo que el eneágono regular no es constructible). Es decir, n tiene que ser de la forma n = siendo r 0, k 0 y primos de Fermat distintos entre sí. Por tanto, el heptágono, el eneágono, el 11-ágono, el 13-ágono y el 14-ágono regulares no son constructibles con regla y compás; sin embargo, el triángulo equilátero, el cuadrado, el pentágono, el hexágono, el octógono, el decágono, el dodecágono, el 15-ágono, el 16-ágono, el heptadecágono regulares sí lo son. Así que sabemos perfectamente qué polígonos regulares son constructibles con regla no graduada y compás; otra cosa distinta será encontrar un procedimiento -usando regla no graduada y compás- que lo construya. 2. La cuadratura del círculo: construir un cuadrado con regla y compás con igual área que un círculo dado. Este problema aparece en el papiro de Rhind (o de Ahmes) en el 1650 a.C. Muchos matemáticos helenos intentaron resolverlo, sin éxito. Arquímedes probó que, si la cuadratura del círculo era posible, entonces se podía construir un segmento con una longitud idéntica a la de una circunferencia dada y viceversa; esto es, construir un segmento de longitud igual a . Pero tal construcción es imposible, pues Ferdinand von Lindemann probó en 1882 que es un número trascendente y, por ende, también. Hay que citar en este contexto a Lambert, quien en 1761 probó la irracionalidad de . 3. La duplicación del cubo: construir un cubo con regla y compás con un volumen igual al doble de otro cubo dado. También se conoce como el problema de Délos, puesto que el oráculo de Apolo en Delfos dijo que para acabar con una plaga que causó la muerte a una cuarta parte de la población era necesario duplicar el altar cúbico de Apolo. Construyeron un cubo de doble arista que el dado; al no remitir la plaga entendieron que esa no era la forma de duplicar el volumen del cubo. Este problema generaliza un resultado conocido, a saber, la duplicación del área de un cuadrado dado, cuya solución consiste en levantar un cuadrado sobre la diagonal del primero. Muchos grandes matemáticos estudiaron el problema durante siglos. Huygens encontró tres métodos de construcción en 1654 y Newton halló diversas formas en 1707, pero tales construcciones no empleaban la regla no calibrada y el compás como únicos instrumentos. Finalmente, Wantzel probó en 1837 que no es posible construir con regla y compás un segmento de longitud igual a . La explicación se encuentra en la teoría algebraica de grupos (de Galois): como tal número es solución de una ecuación cúbica, (por lo que es algebraico), no es constructible más que en el espacio de tres dimensiones y no en el plano.
Bibliografía: Tema 69 de las Oposiciones de 2018 y www.gaussianos.com/construcciones-con-regla-y-compas-iii-los-poligonos-regulares/Duplicación del área de un cuadrado dado (el negro)
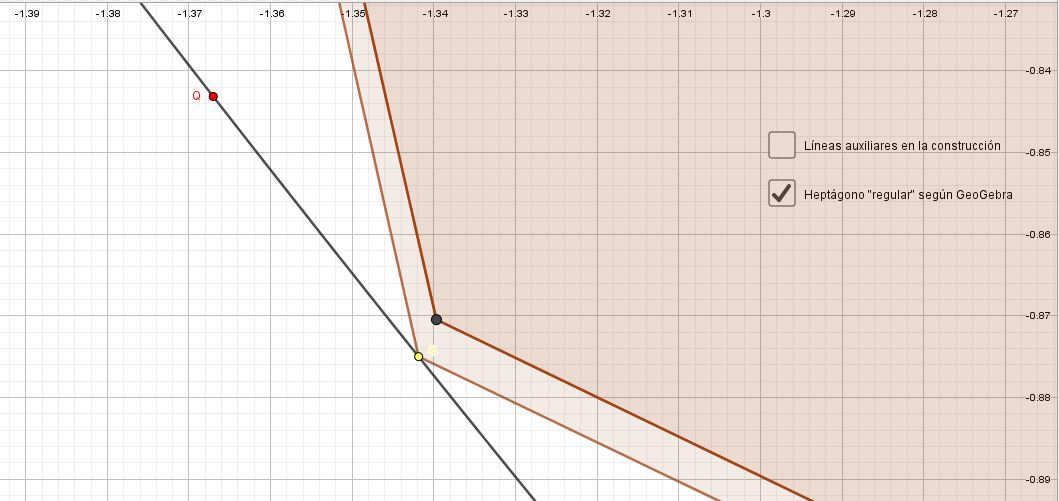
El heptágono regular no es constructible (ni GeoGebra puede)
El heptágono regular no es constructible (ni GeoGebra puede)
El heptadecágono regular sí es constructible, por ser un número primo de Fermat: 17 = 1+ 2^(2^2). Se muestra un procedimiento con regla no graduada y compás para construirlo:

Una de las construcciones de polígonos regulares con regla y compás más conocidas es la del heptadecágono regular (polígono regular de lados).
La primera demostración de que esta construcción es posible se debe también a Gauss, que la encontró cuando contaba con 19 años de edad, aunque parece ser que la primera construcción física de este polígono se debe a Johannes Erchinger. Se piensa que el hecho de encontrar la solución a este problema (que aparece en la sección VII de Disquisitiones Arithmeticae) hizo que Gauss se decantara por las matemáticas en vez de por la filosofía. Quizá sea ésta la razón por la que mandó que se grabara un heptadecágono regular en su tumba, aunque al final el sepulturero encargado del asunto, al ver la dificultad de la construcción y que apenas se distinguiría de un círculo, no lo hizo.