Función parabólica

También podemos encontrar funciones en la guerra. Prueba a manipular las siguientes variables del tanque y averigua qué función sigue su disparo.

Efectivamente, se trata de un movimiento parabólico que podemos representar a través de una función polinómica de segundo grado. Vamos a estudiar la función parabólica, pero antes ¿no habíamos visto ya en geometría lo que es una parábola? A ver si te ayuda esta imagen a refrescar la memoria...

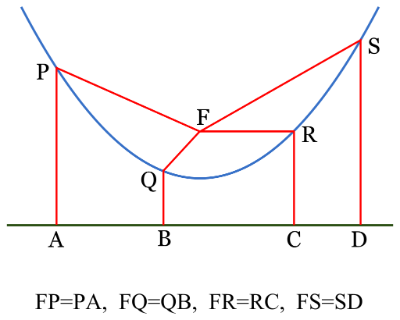
Para construir una parábola necesitábamos dos elementos elementos: el foco y la directriz. Con estos dos elementos podemos definir la parábola como el conjunto de todos los puntos cuya distancia desde el foco es igual a la distancia desde su directriz.

¡Bien! Hecho el repaso, vamos a meternos con las funciones parabólicas Las parábolas son funciones polinómicas de segundo grado que tiene la forma: ¿Cómo se puede representar esta ecuación? ¡Vamos a tratar de entender sus términos! En primer lugar, podemos saber si la parábola se abre hacia arriba o hacia abajo a través del signo de a.

• Si a > 0, la parábola se abre hacia arriba.
• Si a < 0, la parábola se abre hacia abajo.